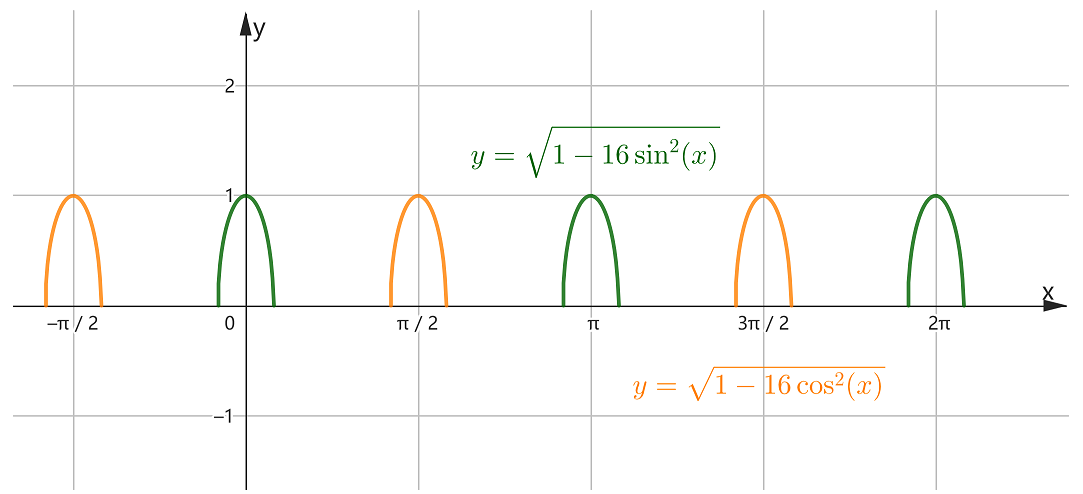第2295题：椭圆周长

本题再从头推导上一题中的椭圆周长积分公式，对椭圆 $\begin{cases} x=a \cos t, \\ y=b \sin t \end{cases}$ ，

令 $c=\sqrt{a^2-b^2}$ ，离心率 $\epsilon=\dfrac{c}{a}$ ，

其全长为

$s1=$ $\int_0^{2\pi} \sqrt{ a^2 \sin^2 t +b^2 \cos^2 t } dt$

$=\int_0^{2\pi} \sqrt{ a^2 -c^2 \cos^2 t } dt$

$=a\int_0^{2\pi} \sqrt{1 -\epsilon^2 \cos^2 t } dt$ ⑴

$=a\int_0^{2\pi} \sqrt{1 -\epsilon^2 \sin^2 t }$ $dt$   ⑵

接下来，对比一下正弦曲线 $y=c \sin \dfrac{x}{b}$ 的一波之长（ $0 \leqslant x \leqslant 2\pi b$ ）

$s2=$ $\int_0^{2\pi b} \sqrt{1+\dfrac{c^2}{b^2} cos^2 \dfrac{x}{b}} dx$

令$t=\dfrac{x}{b}$

$s2=$ $\int_0^{2\pi} \sqrt{b^2+c^2 \cos^2 t} dt$

$=\int_0^{2\pi} \sqrt{a^2 - c^2 \sin^2 t} dt$

$=a\int_0^{2\pi} \sqrt{1-\epsilon^2 \sin^2 t } dt$ ⑶

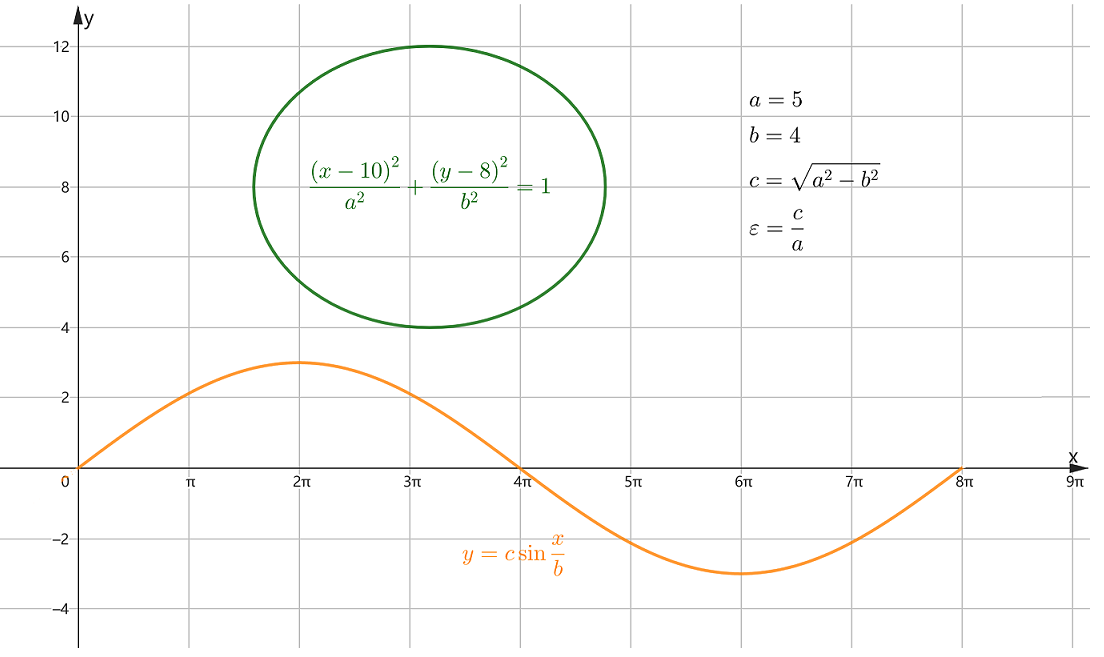
对比 ⑵ 式和 ⑶ 式，椭圆周长和正弦曲线 $y=c \sin \dfrac{x}{b}$ 的一波之长相等.

举例如下图，图中橙色和绿色两曲线弧线长相等.

那么，椭圆周长还和下面哪个曲线的一波之长相等？

A. $y=c \cos \dfrac{x}{b}$ （ $0 \leqslant x \leqslant 2\pi b$ ）

B. $y=c \sin \dfrac{x}{a}$ （ $0 \leqslant x \leqslant 2\pi a$ ）

C. $y=a \sin \dfrac{x}{c}$ （ $0 \leqslant x \leqslant 2\pi c$ ）

D. $y=b \cos \dfrac{x}{c}$ （ $0 \leqslant x \leqslant 2\pi c$ ）

注：

推导过程中⑴式到⑵式的变化无法（至少我本人无法）直接推得，但可以从图形上得到解释，如下图

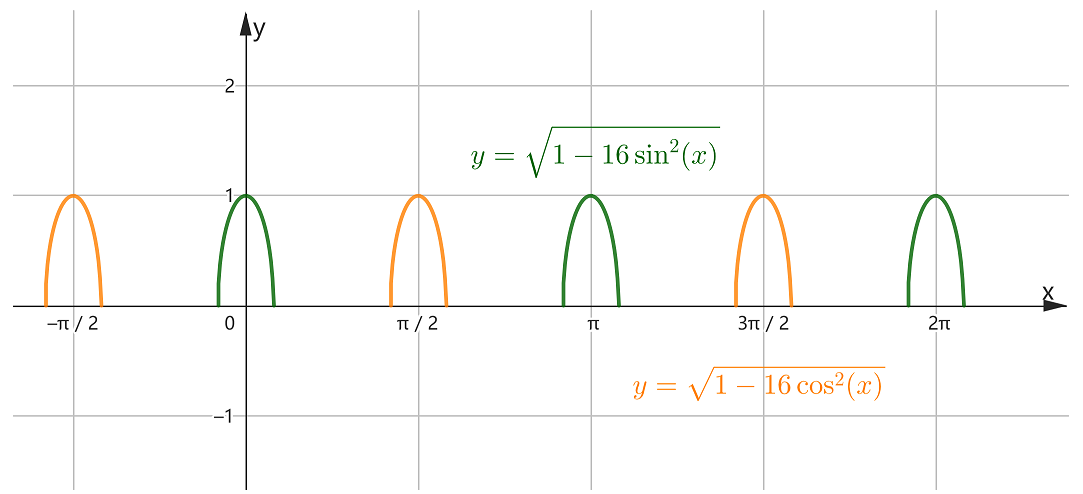
图中设 $\epsilon=4$ ，在 $[0,2\pi]$ 区间内橙色和绿色曲线弧长相等.

注2：⑴式到⑵式，取x=\dfrac{\pi}{2} -t 换元得到. (函数的连续膜)