第2140题：填空

矩阵 $A=\begin{bmatrix} -3 & 1 & 3 & 2 \\ 1 & 4 & 2 & -5 \end{bmatrix}$ 可以将 $\mathbb{R}^4$ 中的一个向量变换成 $\mathbb{R}^2$ 中的一个向量，如

$\begin{bmatrix} -3 & 1 & 3 & 2 \\ 1 & 4 & 2 & -5 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 2 \\ 2 \end{bmatrix}$ $= \begin{bmatrix} 8 \\ -1 \end{bmatrix}$

解方程 $Ax=b$ 就是要求出 $\mathbb{R}^4$ 中所有经过乘以 $A$ 的“作用”后变为 $b$ 的向量 $x$ ，如下图.

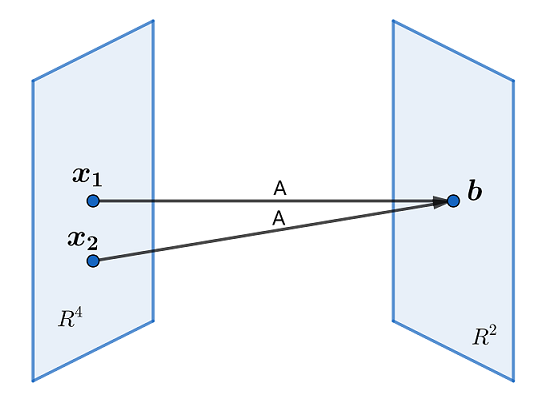
由 $\mathbb{R}^n$ 到$\mathbb{R}^m$ 的一个变换（或称函数、映射）$T$ 是一个规则，它把 $\mathbb{R}^n$ 中每个向量 $x$ 对应以 $\mathbb{R}^m$ 中的一个向量 $T(x)$ . 集 $\mathbb{R}^n$ 称为T的_________，而 $\mathbb{R}^m$ 称为 $T$ 的_________. 对于 $\mathbb{R}^n$ 中向量 $x$ ，$\mathbb{R}^m$ 中向量 $T(x)$ 称为 $x$ 在 $T$ 作用下的像. 所有像$T(x)$ 的集合称为 $T$ 的_________.

A. 定义域，值域，余定义域

B. 值域，余定义域，定义域

C. 余定义域，定义域，值域

D. 定义域，余定义域，值域

余定义域也称为取值空间.