第2284题：用定积分计算旋转体体积

旋转体是由一个平面图形绕这个平面内一条直线旋转一周而成的立体。这条直线叫旋转轴。

如下图，旋转体可以看作是由连续曲线 $y=f(x)$ 、直线 $x=a$ 、 $x=b$ 及 $x$ 轴所围成的曲边梯形绕 $x$ 轴旋转一周而成的立体。

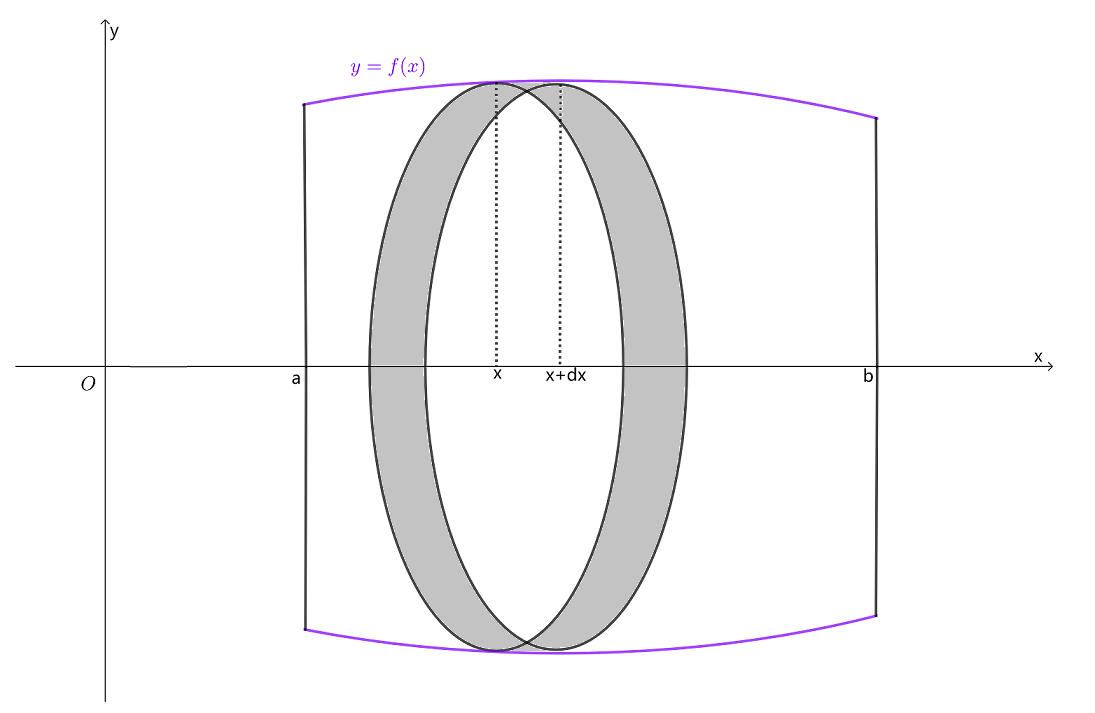
取横坐标 $x$ 为积分变量，它的变化区间为 $[a,b]$ ，相应于 $[a,b]$ 上任一小区间 $[x,x+dx]$ 的窄曲边梯形绕x轴旋转而成的薄片的体积近似于以 $f(x)$ 为底半径、$dx$ 为高的扁圆柱体的体积，即体积元素

$dV=\pi [f(x)]^2 dx$

以 $\pi [f(x)]^2 dx$ 为被积表达式，在闭区间 $[a,b]$ 上作定积分，便得所求旋转体体积为

$V=\int_a^b \pi [f(x)]^2 dx$

下图是正弦曲线 $y=\sin x$ 在 $[0,\pi]$ 区间内的曲线绕x轴旋转所得立体，

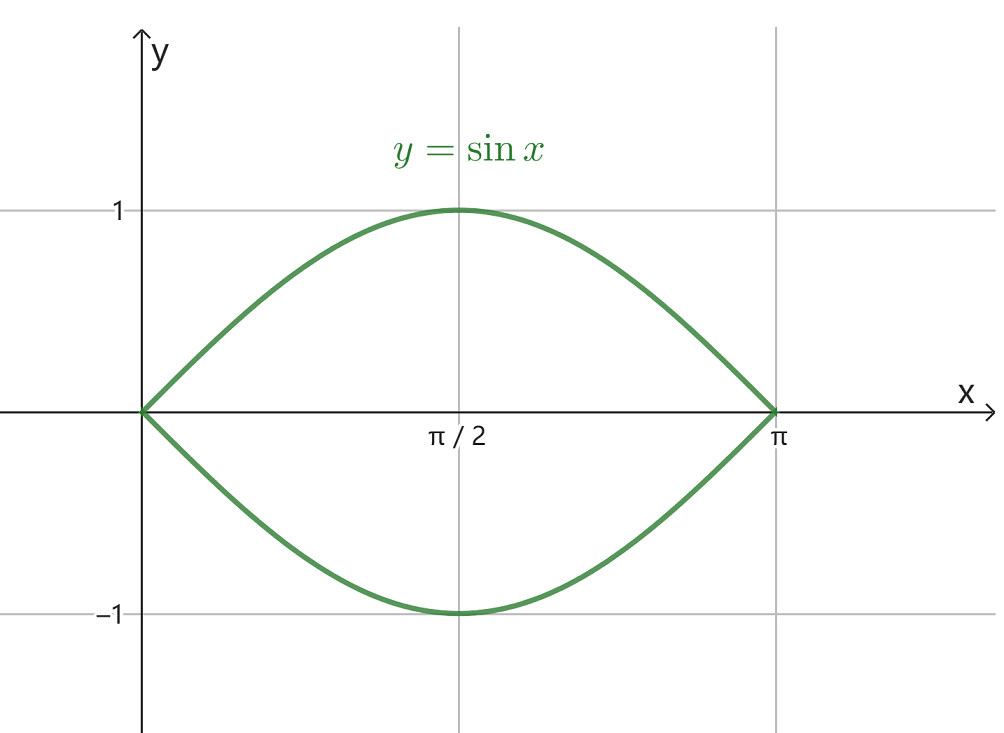
请计算它的体积等于多少？

$V=$$\int_0^{\pi} \pi (\sin x)^2 dx$ $=?$

A. $\dfrac{\pi^2}{4}$

B. $\dfrac{\pi^2}{2}$

C. $\pi^2$

D. $2\pi^2$

注：参考上一题最后的积分公式。