第2286题:扩展阶乘到实数域
的阶乘是多少?将近 年前哥德巴赫提出这个问题,阶乘本是对整数而言的,如 ,将整数及其对应的阶乘画到平面上得到以下不连续的点。
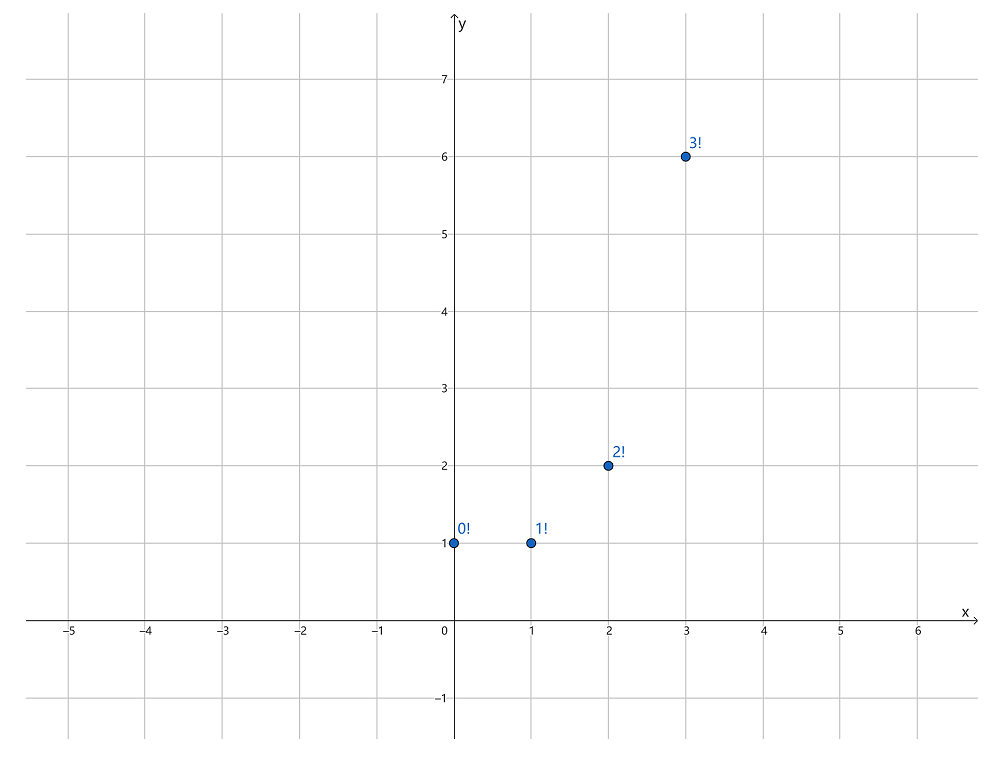
那么,能不能找到一条曲线完美连接这些点呢?就是说,能不能找到一个函数来计算实数的阶乘呢?这一问题被称为泛化阶乘,或阶乘一般化。
哥德巴赫把这个问题留给了伯努利兄弟中的约翰·伯努利,约翰·伯努利曾是欧拉的老师,此问题正好被欧拉看到并最终解决,这就是上一题中的欧拉第二积分,也叫伽玛函数(gamma function),长相如下:
改写一下,
在上一题中关于伽玛函数的性质有一条 ,而其中的 并不必须是整数,这正是阶乘的扩展。
上一题中,画出了 的图形,并不通过整数阶乘点,把图形向左偏移 个单位,画出 的图形如下
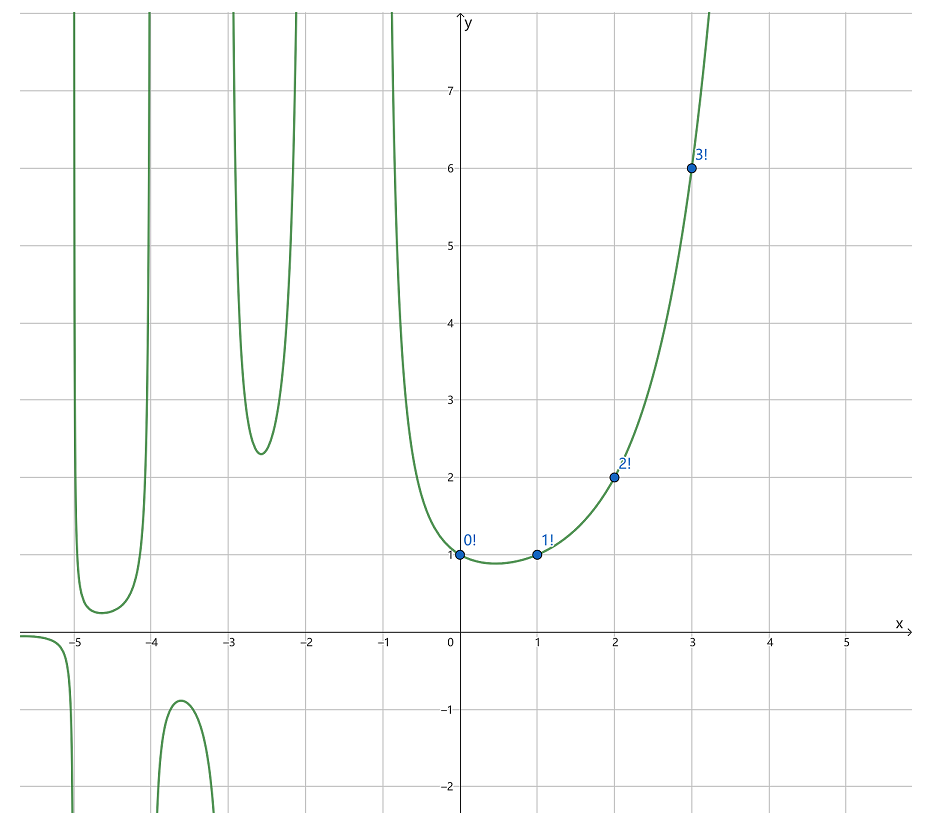
的图形完美通过整数的阶乘点,将阶乘从整数域扩展到了实数甚至复数域。
以下是伽玛函数的一个JavaScrip实现,
function gamma(x)
{
var p = [0.99999999999980993, 676.5203681218851, -1259.1392167224028,771.32342877765313, -176.61502916214059, 12.507343278686905,-0.13857109526572012, 9.9843695780195716e-6, 1.5056327351493116e-7];
var g = 7;
if (x < 0.5) {
return Math.PI / (Math.sin(Math.PI * x) * gamma(1 - x));
}
x -= 1;
var a = p[0];
var t = x + g + 0.5;
for (var i = 1; i < p.length; i++) {
a += p[i] / (x + i);
}
return Math.sqrt(2 * Math.PI) * Math.pow(t, x + 0.5) * Math.exp(-t) * a;
}
可以在电脑记事本里抄写这段代码,复制上,打开一个浏览器,按F12,进入浏览器自带的控制台,粘贴这段代码。回车后,新起一行,输入函数名称传入一个实数,计算得到实数的阶乘。
下面是用Edge浏览器的控制台运行以上代码的截图。
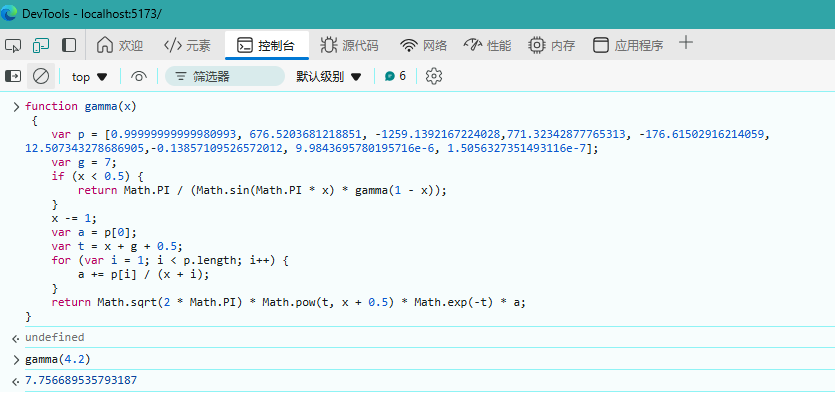
上一题选项中, 的阶乘结果与 有关, 。
猜一下,gamma(6.8) 约等于多少?
A. 85.622
B. 101.27
C. 367.92
D. 496.61
注:
1、《数学长征》正在改版,在下一版中,每一题都有可能附带一个可交互的图形操作或数据计算以加深理解,像本题这样的计算可以在题目里直接交互,敬请关注。
2、如果你想运行一段程序又没有运行环境,可以像本题一样写成JS代码在浏览器中执行。


