第2138题：线性关系的几何意义

从几何意义上看，在 $\mathbb{R}^2$ 空间中：

任意两个向量线性相关，它们必然落在平面直角坐标系中通过原点的同一条直线上. 

任意两个向量线性无关，它们必然落在平面直角坐标系中通过原点的两条不同的直线上.

例如下图中 $A,B$ 两点线性相关，$A,C$ 两点$B,C$ 两点线性无关.

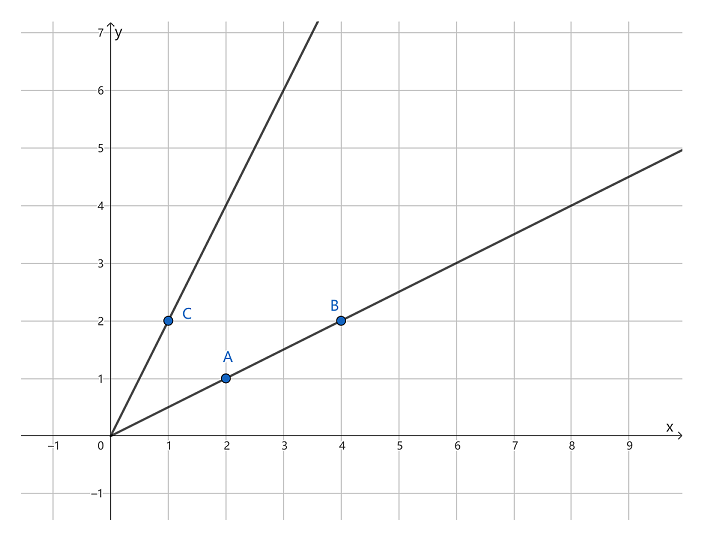
在 $\mathbb{R}^3$ 空间中：

任意两个向量线性相关，它们必然落在(三维)空间直角坐标系中通过原点的同一条直线上.

任意两个向量线性无关，则它们必然落在(三维)空间直角坐标系中通过原点的两条不同的直线上.

若在 $\mathbb{R}^3$ 空间中有三个向量 $u,v,w$ ，以下说法正确的是（  ）.

A. 若 $u,v$ 线性无关，则 $u,v,0$ 三个向量能唯一确定一个平面

B. 若 $u,v$ 线性相关，则 $u,v,0$ 三个向量能唯一确定一个平面

C. 若 $u,v$ 线性无关，$w$ 是 $u,v$ 的线性组合，则 $w$ 在 $u,v,0$ 确定的平面上

D. 若 $u,v$ 线性无关，$w$ 不是 $u,v$ 的线性组合，则 $w$ 在 $u,v,0$ 确定的平面上