第2281题：椭圆的面积

如图

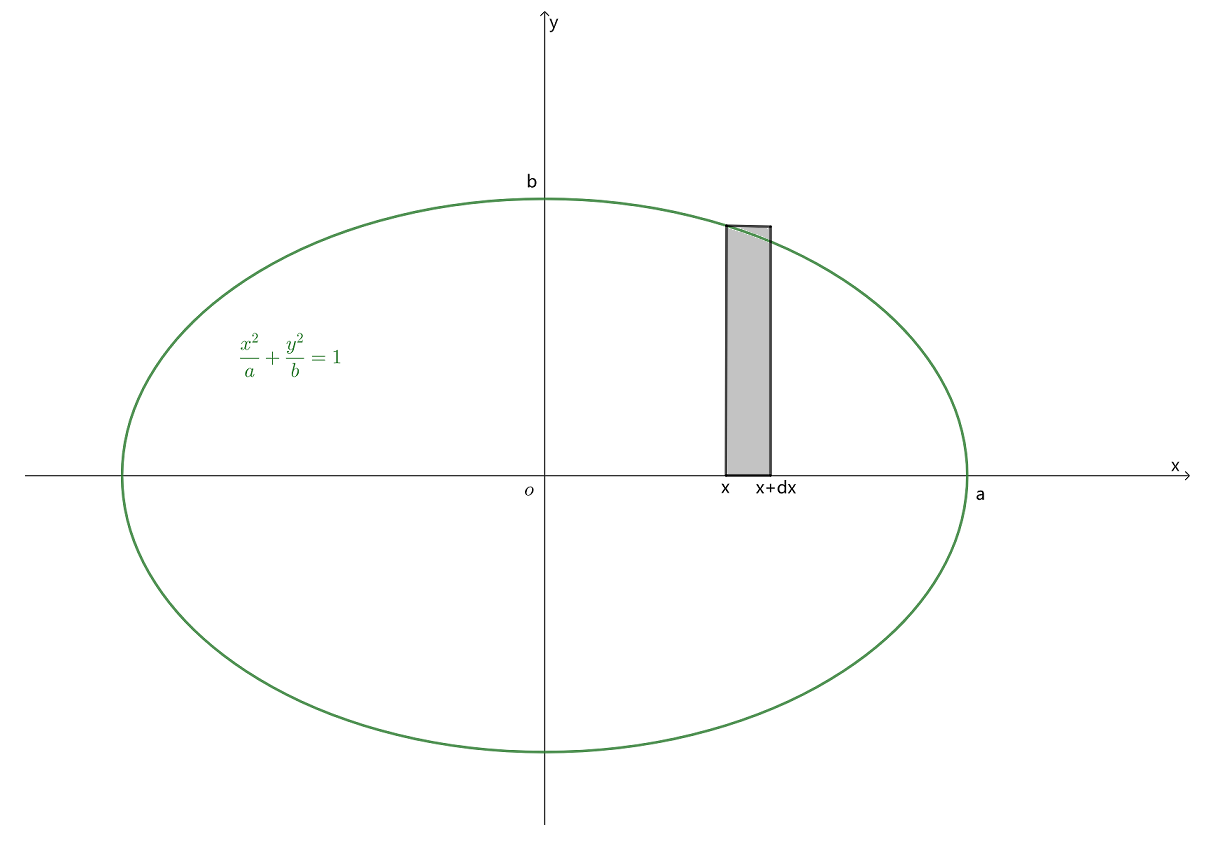
为了求椭圆 $\dfrac{x^2}{a}+ \dfrac{y^2}{b}=1$ 所围棋成的面积 $S$ ，可以先求出第一象限中的两坐标轴与椭圆所围成的面积 $S_1$ 然后乘以 $4$ 。

$S=4S_1=\int_0^a ydx$ .

解出 $y=\dfrac{b}{a} \sqrt{a^2-x^2}$

得到 $S_1=$$\dfrac{b}{a} \int_0^a \sqrt{a^2-x^2}dx$ .

参考积分公式

$\int \sqrt{a^2-x^2}dx =$ $\dfrac{x}{2} \sqrt{a^2-x^2}$ $+ \dfrac{a^2}{2} \arcsin \dfrac{x}{a}$ $+C$

积出 $S_1$ 等于多少？

A. $\dfrac{\pi ab}{4}$

B. $\dfrac{\pi ab}{2}$

C. $\pi ab$

D. $2 \pi ab$

注：也可以用椭圆的参数方程

$\begin{cases} x=a \cos t \\ y=b \sin t \end{cases}$ $(0 \leqslant t \leqslant \dfrac{\pi}{2})$

然后用定积分换元法得到结果。