第2233题：含旋转变换的矩阵

杰克研究了几个特征值为复数的二阶方阵，观察它们对平面上点的作用，例如对于点 $x_0=[2,0]^T$ .

1）

矩阵 $A=\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}$ 的特征值为 $i$ 和 $-i$ .

$x_1=Ax_0=\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 2 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 2 \end{bmatrix}$

$x_2=Ax_1= \begin{bmatrix} -2 \\ 0 \end{bmatrix}$

$x_3=Ax_2=\begin{bmatrix} 0 \\ -2 \end{bmatrix}$

$x_0,x_1,x_2,x_3$ 正好落在圆上，说明$A$ 中包含有旋转变换，见图$1$ .

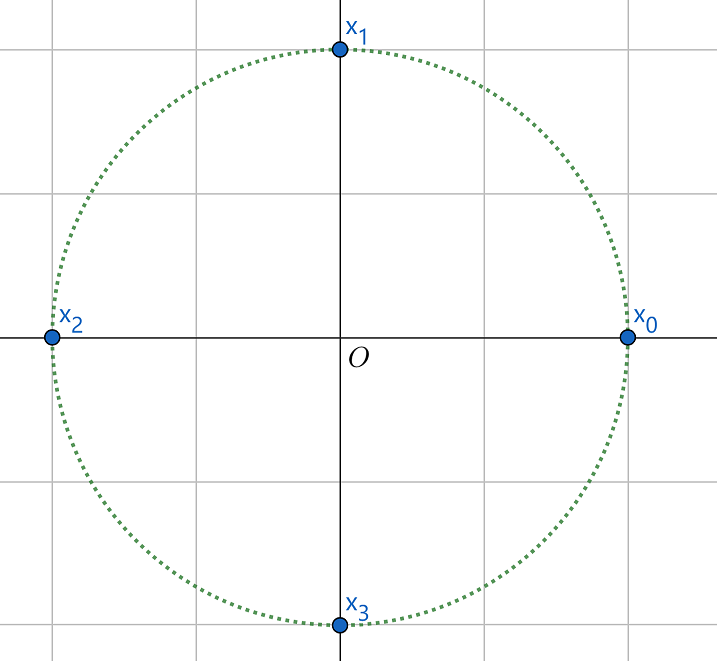
图1

2）

矩阵 $B=\begin{bmatrix} 0.5 & -0.6 \\ 0.75 & 1.1 \end{bmatrix}$ 的特征值为 $0.8+0.6i$ 和 $0.8-0.6i$ .

$x_1=Bx_0= \begin{bmatrix} 1.0 \\ 1.5 \end{bmatrix}$

$x_2=Bx_1= \begin{bmatrix} -0.4 \\ 2.4 \end{bmatrix}$

$x_3=Bx_2= \begin{bmatrix} -1.64 \\ 2.34 \end{bmatrix}$

……

一直算下去，发现这些点落在一个椭圆上，说明$B$ 中包含有旋转变换，见图$2$ .

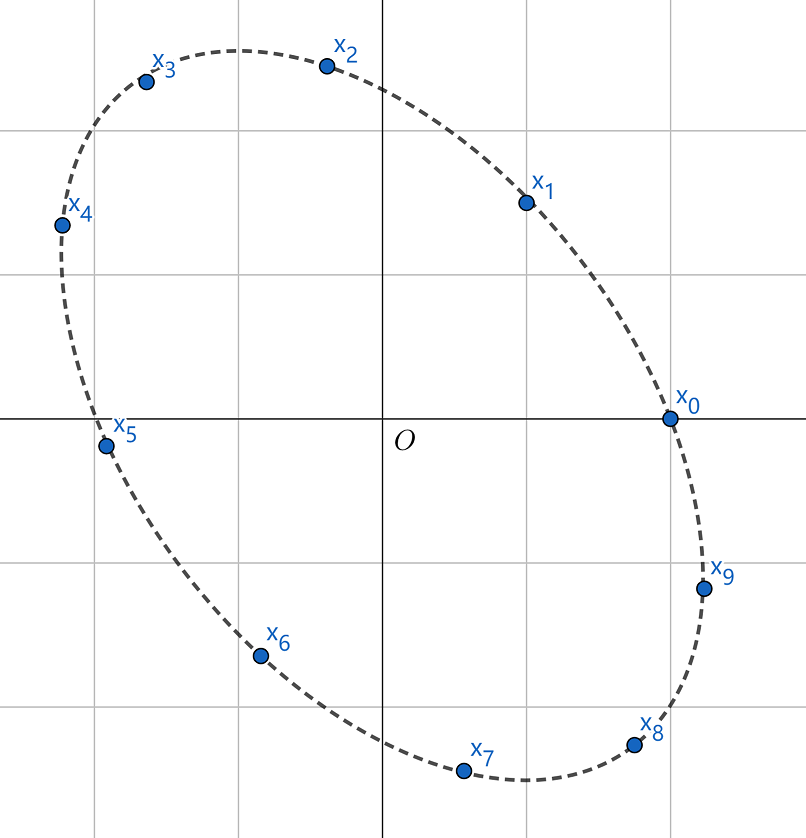
图2

3）

矩阵 $C=\begin{bmatrix} 2 & -3 \\ 1 & 2 \end{bmatrix}$ 的特征值为 $2+\sqrt{3}i$ 和 $2-\sqrt{3}i$

$x_1=Cx_0= \begin{bmatrix} 4 \\ 4 \end{bmatrix}$

$x_2=Cx_1= \begin{bmatrix} -4 \\ 12 \end{bmatrix}$

$x_3=Cx_2= \begin{bmatrix} -44 \\ 20 \end{bmatrix}$

……

一直算下去，这些点画出类似螺旋线的图形，说明$C$ 中包含有旋转变换，见图$3$ .

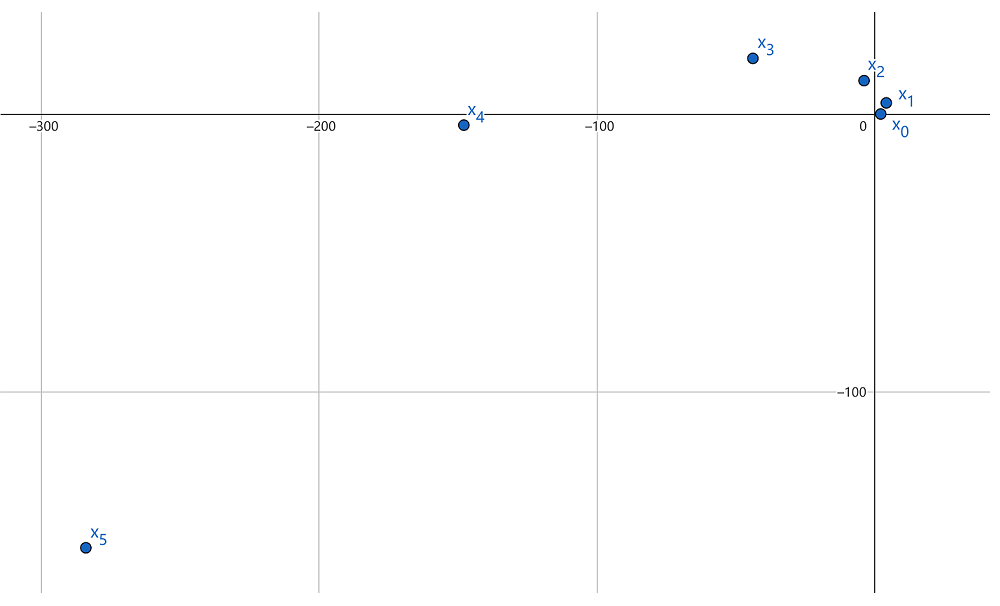
图3

4）

但是对于特征值为实数的矩阵，可以简单找到一个不含有旋转变换的矩阵，

例如矩阵 $D=\begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix}$ 的特征值为 $0$ 和 $2$ .

$x_1=Dx_0= \begin{bmatrix} 2 \\ 2 \end{bmatrix}$

$x_2=Dx_1= \begin{bmatrix} 4 \\ 4 \end{bmatrix}$

$x_3=Dx_2= \begin{bmatrix} 8 \\ 8 \end{bmatrix}$

……

$D$ 对点的作用只有位移和拉伸变换，没有旋转变换，见图 $4$ .

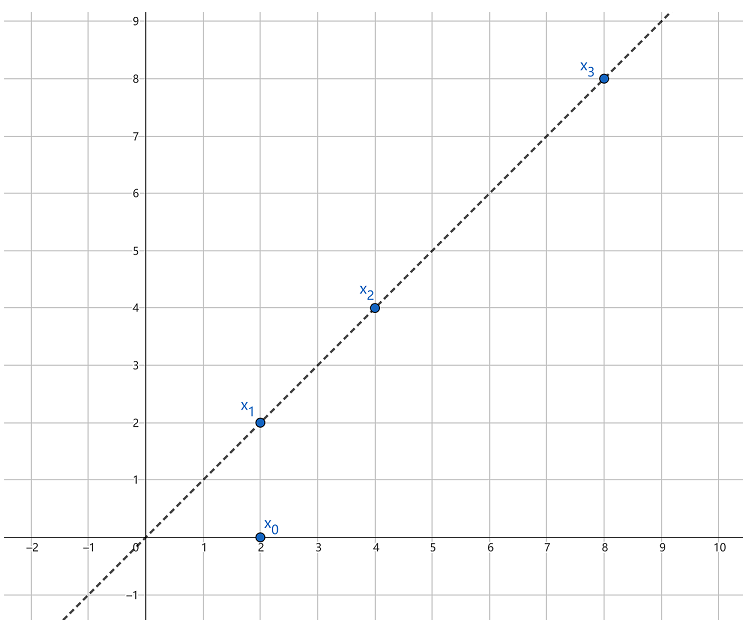
图4

因此，

杰克得到一个结论：特征值为非实数的矩阵必定含有旋转变换. 对吗？

恭喜坚持到近2200题！线性代数第一部分即将完结。