第2382题：欧拉常数

当 $f(x)$ 是减函数时，利用类似上题的方法可以得到更精密的结果.

设 $x \geqslant m \in \mathrm{N}^*$ 时，f是一个非负的递减函数，则极限

$\displaystyle {\lim_{n \to \infty} \Big ( \sum_{k=m}^{n-1} f(k) -\int_m^n f(x) dx \Big ) }=\alpha$ （1）

存在，且 $0 \leqslant \alpha \leqslant f(m)$ . 更进一步，如果 $\displaystyle {\lim_{n \to +\infty} f(x)} =0$ ，那么

$\Big | \displaystyle { \sum_{k=m}^{[\xi]} f(k) -\int_m^{\xi} f(x) dx -\alpha } \Big | \leqslant f(\xi -1)$  （2）

其中 $\xi \geqslant m+1$ .

调和级数

$H_n=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\cdots+\dfrac{1}{n}$

是发散的，随着 $n$ 越来越大，级数的和 $H_n$ 趋向于无穷大，但是增长的非常缓慢.

另一个增长缓慢的函数是自然对数函数 $\ln(n)$ ，当 $n$ 越来越大 $\ln(n)$ 也趋向于无穷大，如下图

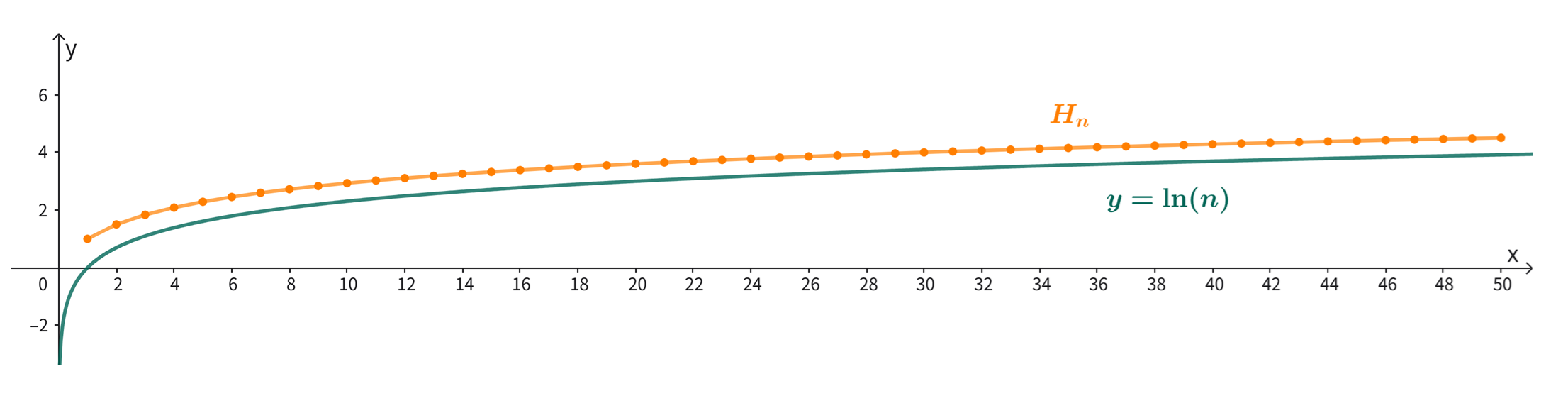
从图上看，它们增长的速率几乎相同，以至于它们的差 $H_n - \ln(n)$ 并不会趋向于无穷大，而是会收敛到一个固定的数值，这个数值就是有名欧拉常数$\gamma$ ，其定义如下

$\gamma=\displaystyle{\lim_{n \to \infty} \Big ( \sum_{k=1}^ {n-1} \dfrac{1}{k} - \ln n \Big )}$  （3）

在公式（1）中，取 $f(x)=\dfrac{1}{x}$ ，$m=1$ ，即得到公式（3）.

$\gamma \approx 0.57721566$ ，目前尚不确定它是不是有理数.

由欧拉常数的定义，可得不等式（ ）.

A. $H_n -1 < \ln(n) < H_{n-1}$

B. $H_n -1 \leqslant \ln(n) \leqslant H_{n-1}$

C. $\ln(n) > H_{n-1}>H_n -1$

D. $\ln(n) \geqslant H_{n-1} \geqslant H_n -1$

参考：2335题，另：对空集求和默认为0.

参考：常庚哲 史济怀《数学分析教程》（上）第七章.