第2256题:定积分的近似计算
定积分有几种近似计算方法,第一种是矩形法,如下图,其几何意义是用窄条矩形的面积作为窄条曲边梯形面积的近似值。整体上用台阶形的面积作为曲边梯形面积的近似值。
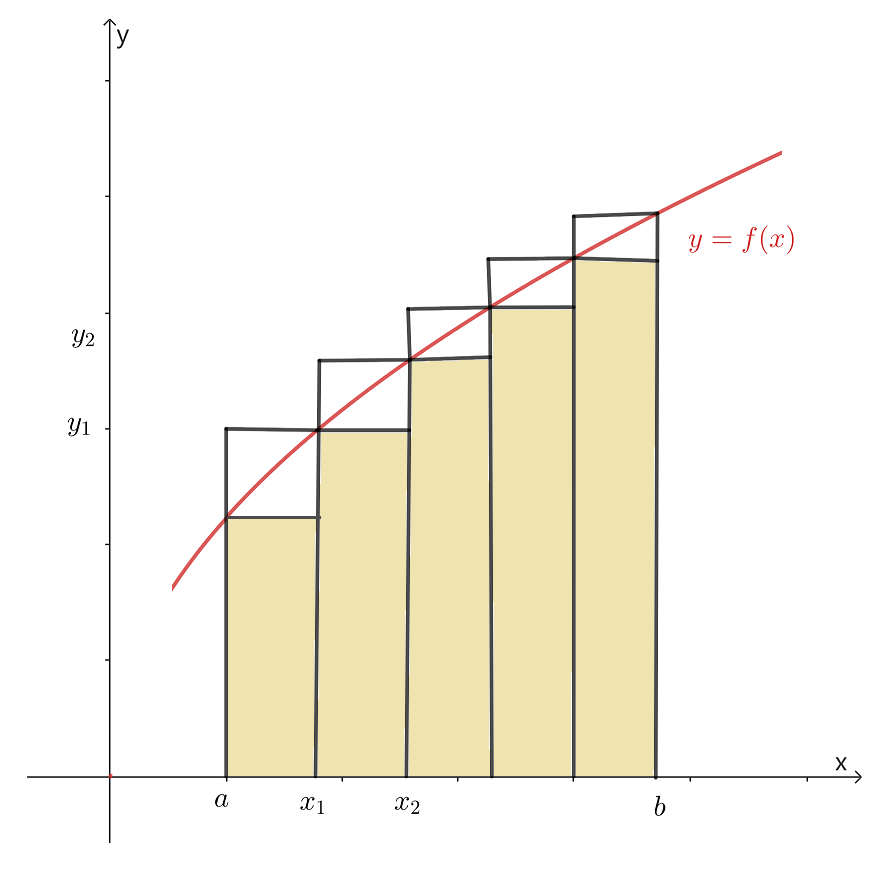
图1
将曲线 分解成 份窄条矩形,得到一系列 后,可以用以下近似公式计算定积分:
已知
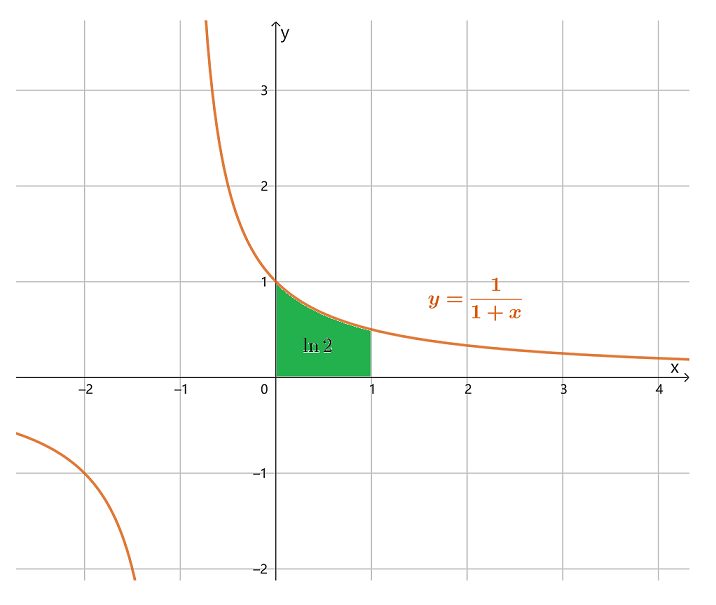
图2
取 ,计算 得
请用以下 个矩形数据套入矩形法计算 的近似值,结果取四位小数。
| 0 | 1 | 2 | 3 | 4 |
| 0.0000 | 0.1000 | 0.2000 | 0.3000 | 0.4000 |
| 1.0000 | 0.9091 | 0.8333 | 0.7692 | 0.7143 |
| 5 | 6 | 7 | 8 | 9 |
| 0.5000 | 0.6000 | 0.7000 | 0.8000 | 0.9000 |
| 0.6667 | 0.6250 | 0.5882 | 0.5556 | 0.5263 |
结果明显大于0.6931的原因是,对于图2曲线,每个小窄条矩形面积都大于对应的曲边梯形面积。
而对于图1曲线,每个小窄条矩形面积都小于对应的曲边梯形面积。


