第2238题：最小二乘问题

定义：如果 $m \times n$ 矩阵 $A$ 和向量 $b$ 属于 $\mathbb{R}^n$ ，$Ax=b$ 的最小二乘解是 $\mathbb{R}^n$ 中的 $\hat{x}$ ，使得

$||$ $b- A \hat{x}$ $||$ $\leqslant$ $|| b-Ax ||$

对所有$x \in \mathbb{R}^n$ 成立.

如下图，最小二乘问题最重要的特征是无论怎么选取 $x$ ，向量 $Ax$ 必然属于列空间 $Col A$ ，对 $x$ ，$b$ 与 $A \hat{x}$ 的距离小于与其它 $Ax$ 的距离.

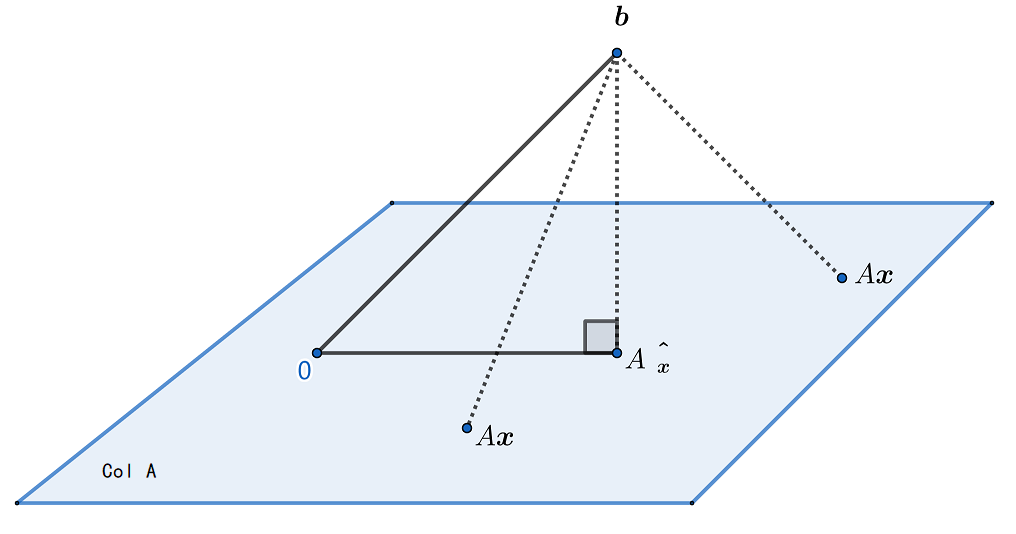
可以证明， 方程 $Ax=b$ 的最小二乘解集和方程 $A^T Ax=A^T b$ 的非空解一致. $A^T Ax=A^T b$ 表示的线性方程给通常称为 $Ax=b$ 的法方程. 解之得到

$\hat{x}=(A^T A)^{-1} A^T b$ .

已知

$A=\begin{bmatrix} 4 & 0 \\ 0 & 2 \\ 1 & 1 \end{bmatrix}$ , $b=\begin{bmatrix} 2 \\ 0 \\ 11 \end{bmatrix}$ ，

求 $Ax=b$ 的最小二乘解 $\hat{x}$ .

A. $\hat{x}=\begin{bmatrix} 0 \\ 1 \\ 2 \end{bmatrix}$

B. $\hat{x}=\begin{bmatrix} 2 \\ 0 \\ 1 \end{bmatrix}$

C.$\hat{x}=\begin{bmatrix} 2 \\ 1 \end{bmatrix}$

D. $\hat{x}=\begin{bmatrix} 1 \\ 2 \end{bmatrix}$