第2252题：定积分的近似计算三

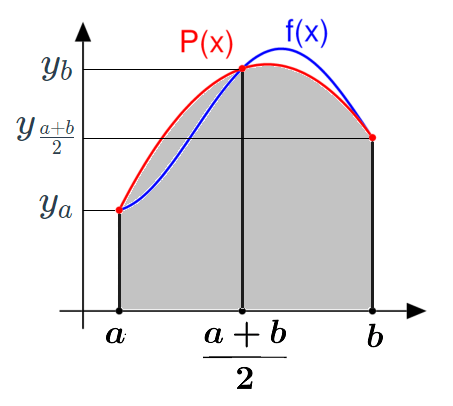
定积分近似计算第三种方法是抛物线法，也叫辛普森（Simpson）法。如下图，其原理是将曲线f(x)上的弧段两等分后用抛物线P(x)近拟代替。下图中以 $[a,b]$ 为底的曲边梯形面积为

$\dfrac{b-a}{3n}$ $(y_a+4 y_{\frac{a+b}{2}}+y_b)$   $(n=2)$

取 $n$ 为偶数，得到定积分的近似值为

$\int_{a}^{b} f(x)dx \approx$ $\dfrac{b-a}{3n} [y_0+y_n$ $+4(y_1+y_3+\cdots + y_{n-1})$ $+ 2(y_2+y_4+ \cdots + y_{n-2})]$

仍用上一题计算 $\ln 2 =\int_{0}^{1} \dfrac{x}{1+x} dx$ 的近似数据计算。

请将以上数据套入抛物线法公式计算 $\ln 2$ 的近似值 $(n=10)$ ，结果保留 $4$ 位小数。

可以看出抛物线法比梯形法精度更高。