第2240题：回归直线

通过前两题，我们知道“最小二乘”实际上是找出使 $\| b-Ax \|$ 尽量小的 $x$ ，当 $b$ 指代一个点，$Ax$ 指代一条线时，指点到直线的最近距离。当 $b$ 指代一个点，$Ax$ 指代一个面时，指点到平面的最近距离，最小二乘法也称为最小平方法，“二乘”其实就是乘二次，即平方。

在最小二乘法中，我们试图找到一条最佳的直线或曲线来拟合给定的数据点。“最佳”的含义在于，这条线或曲线应该尽可能地靠近所有的数据点。然而，这条线或曲线可能无法完美地穿过所有的数据点。所以需要一种方法来衡量线或曲线与数据点的接近程度。

最小二乘法提供了一种衡量方法：对于每个数据点，我们计算它与线或曲线的距离，然后将这个距离的平方进行求和。这就是“最小二乘法”名字的由来——我们试图找到一条线或曲线，使得这个“平方和”或“二次和”尽可能小。

总结来说，“最小二乘法”中的“最小”是指尽可能地使得所有数据点与拟合线（或曲线）的距离的平方和最小，见下图

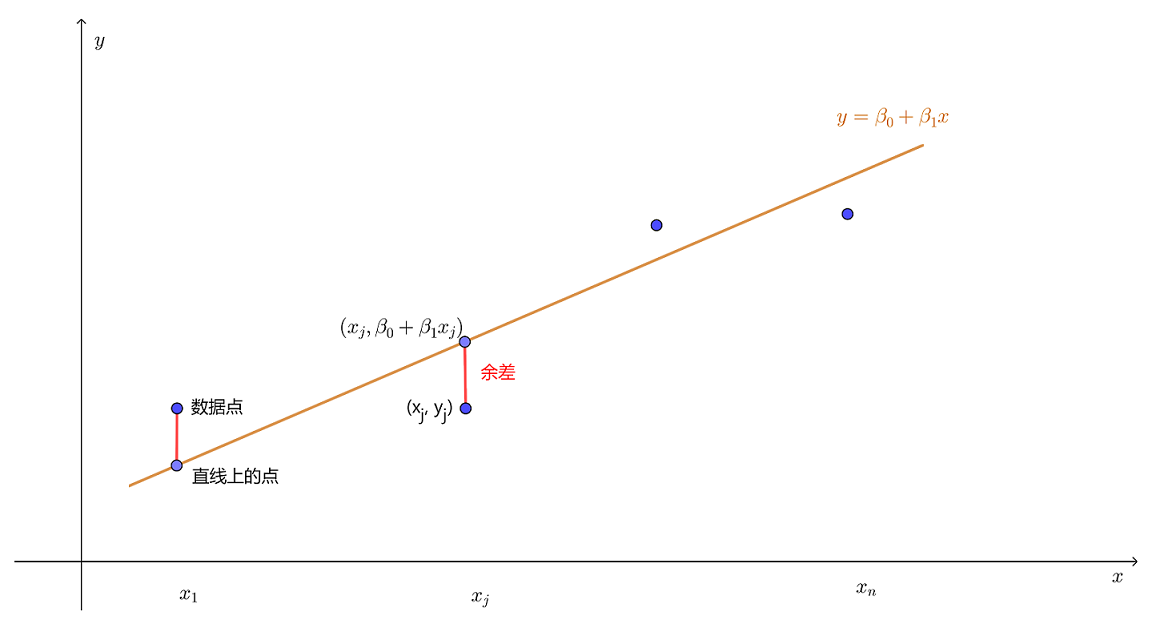
数据点（ $y_j$ ）与拟合点（ $\beta_0 +\beta_1 x_j$ ）之间的距离称为余差，最小二乘直线是余差平方和最小，这条直线也称为 $y$ 对 $x$ 的回归直线，系数 $\beta_0$ ，$\beta_1$ 称为回归系数。

如果数据点都在直线上，方程 $X \beta =y$ 有解，反之，如果数据点不在一条直线上，计算 $X \beta =y$ 的最小二乘问题等价于找出向量组 $\beta$ ，确定出上图中的最小二乘直线。

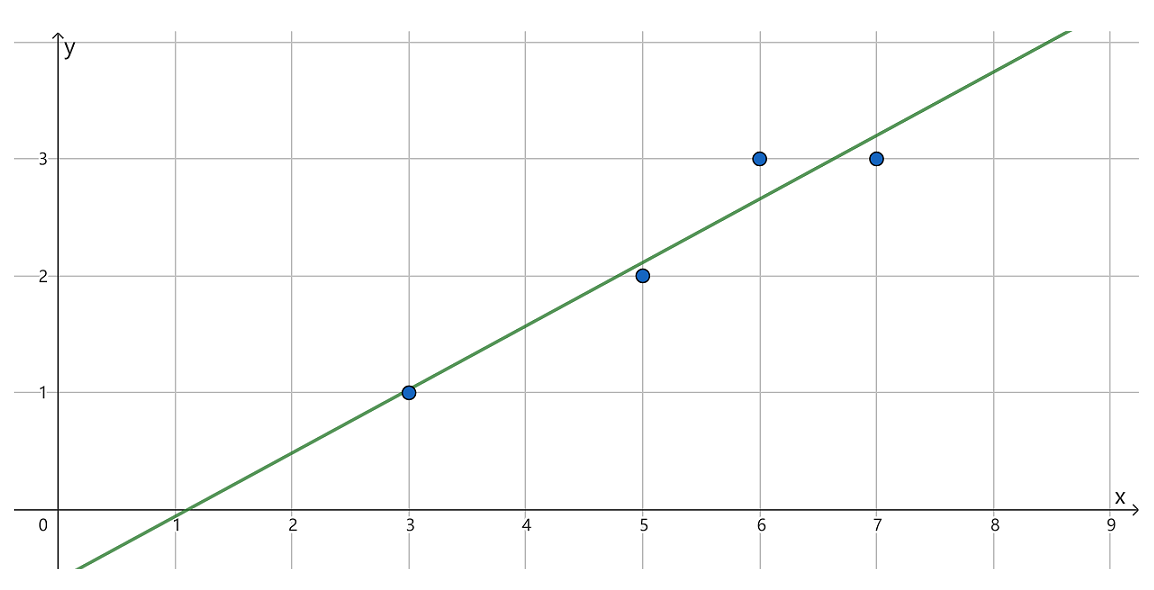
设有一组数据 $(3,1),(5,2)$ $,(6,3),(7,3)$ ，为计算最小二乘直线，构造矩阵 $X$ 和向量 $y$ :

$X=\begin{bmatrix} 1 & 3 \\ 1 & 5 \\ 1 & 6 \\ 1 & 7 \end{bmatrix}$ ，$y=\begin{bmatrix} 1 \\ 2 \\ 3 \\ 3 \end{bmatrix}$

通过解 $X \beta =y$ 得到回归系数。

解法大致如下：

1） $X^T X \beta =X^T y$

2）$\beta= (X^T X)^{-1} X^T y$

3）得到 $y=\beta_0+ \beta_1 x$

则 $\beta_0$ ，$\beta_1$ 分别为（ ）。

A. $\beta_0= -\dfrac{2}{7}, \beta_1=\dfrac{9}{14}$

B. $\beta_0= \dfrac{2}{7}, \beta_1=\dfrac{9}{14}$

C. $\beta_0=-\dfrac{3}{5}, \beta_1=\dfrac{19}{35}$

D. $\beta_0= \dfrac{3}{5}, \beta_1=\dfrac{19}{35}$

据此做出回归直线如下图：