第2387题:估计和式的大小
面积原理是用积分来估计和式,如图1,推导曲线下的面积时,用一系列小矩形(或梯形)的和逼近,当小矩形步长足够小时,曲线下的面积可以准确求得. 反过来,这些矩形面积和的大小就可以用曲线下的面积来估计.
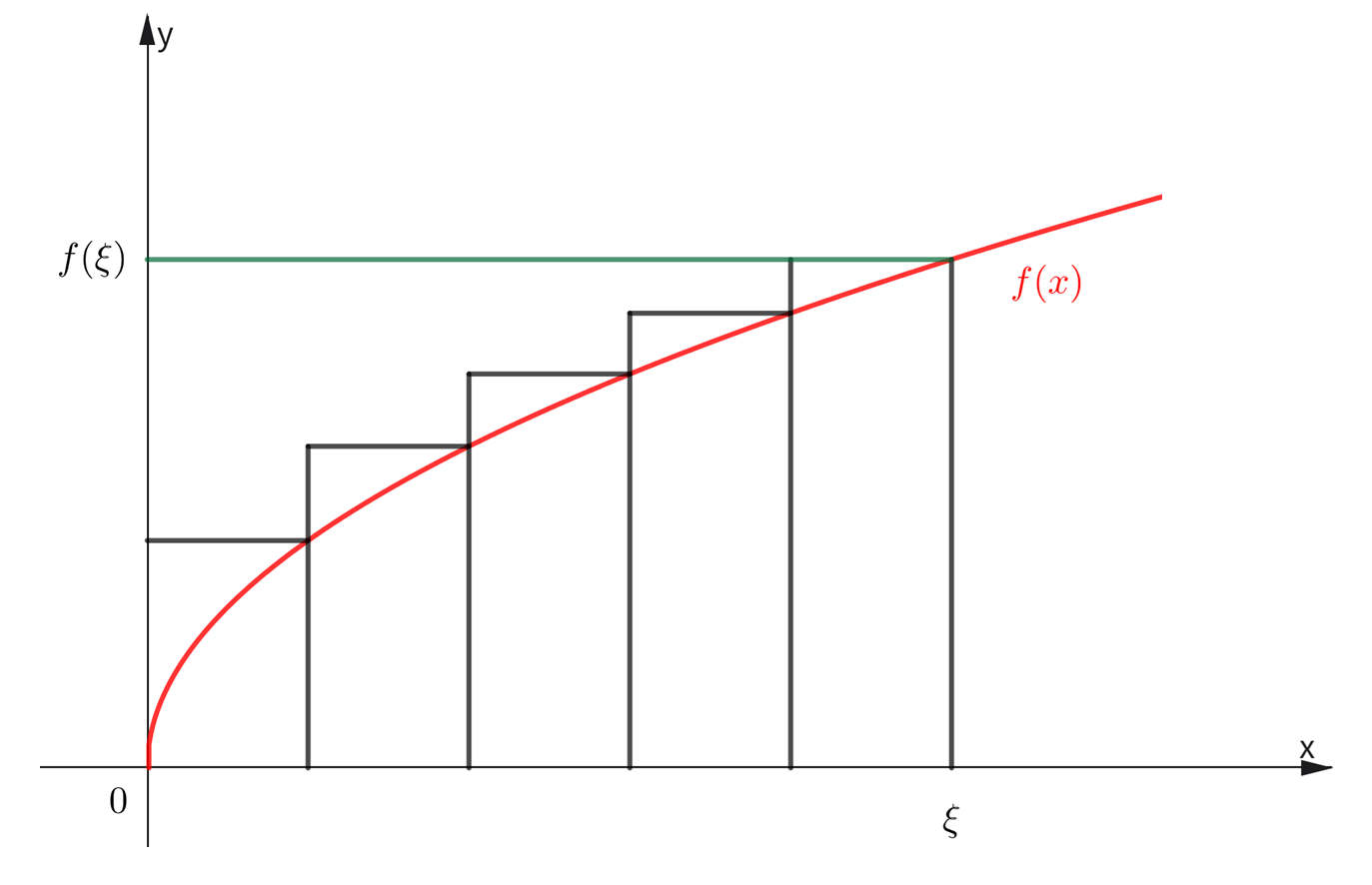
如图2,设 f(x) 是一个非负的增函数,在积分区间内(本题为 [0,ξ] ),从几何意义上来说,有以下定理:所有小矩形面积之和减去曲线下面积后结果小于等于 f(x) 在 ξ 点对应的函数值,可以表达为( ).
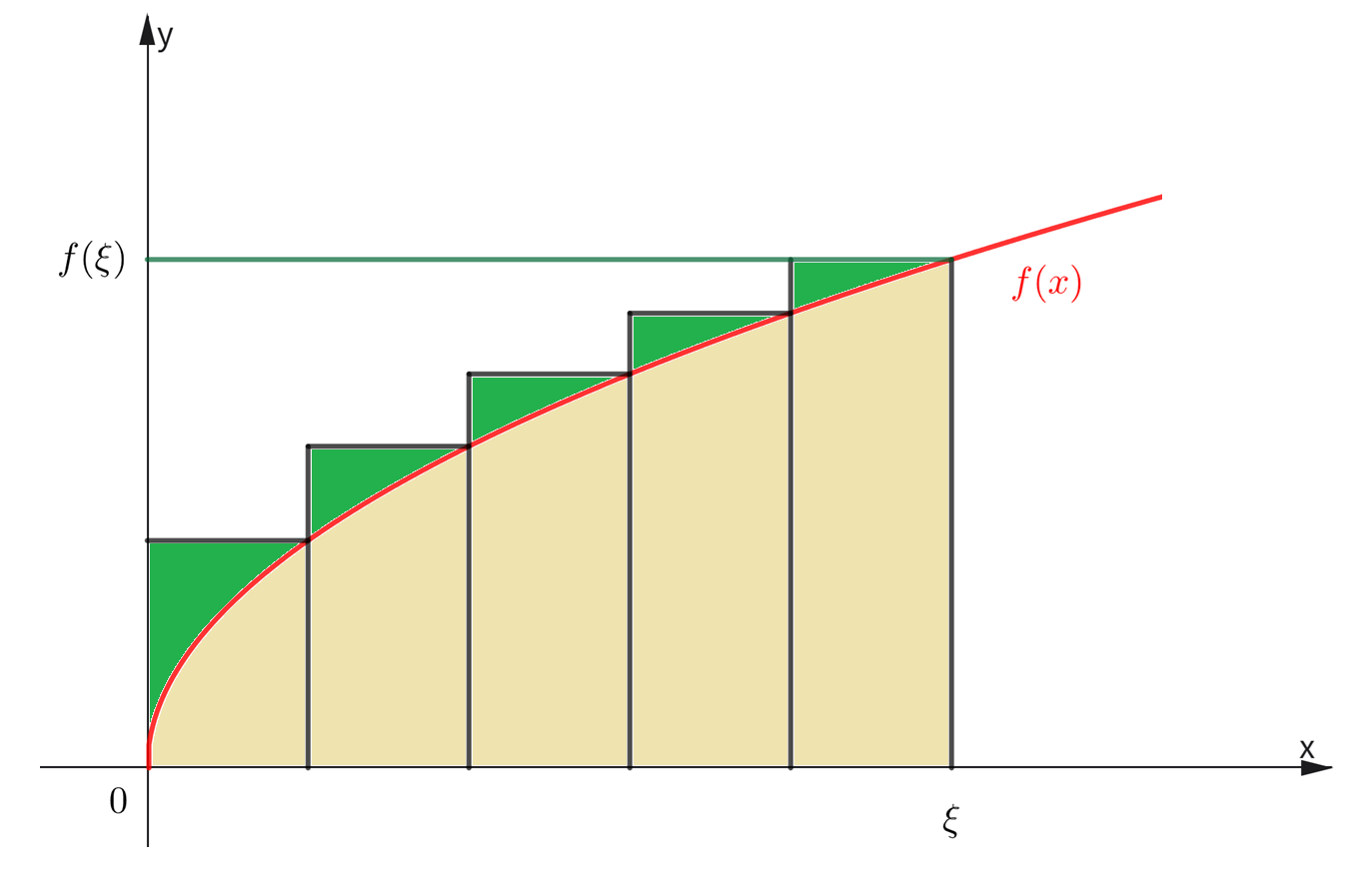
A. ∣∣∣k=1∑ξf(k)−∫1ξf(x)dx∣∣∣=0
B. ∣∣∣k=1∑ξf(k)−∫1ξf(x)dx∣∣∣⩽f(ξ)
C. ξ→∞lim(k=1∑ξf(k)−∫1ξf(x)dx)=0
D. ξ→∞lim(k=1∑ξf(k)−∫1ξf(x)dx)⩽f(ξ)
题中求和上限应该是[ξ] ,因为小矩形只能是整数个。




