第2291题:椭球体体积
下图是由椭圆
所围成的图形绕x轴旋转一周而成的旋转椭球体.
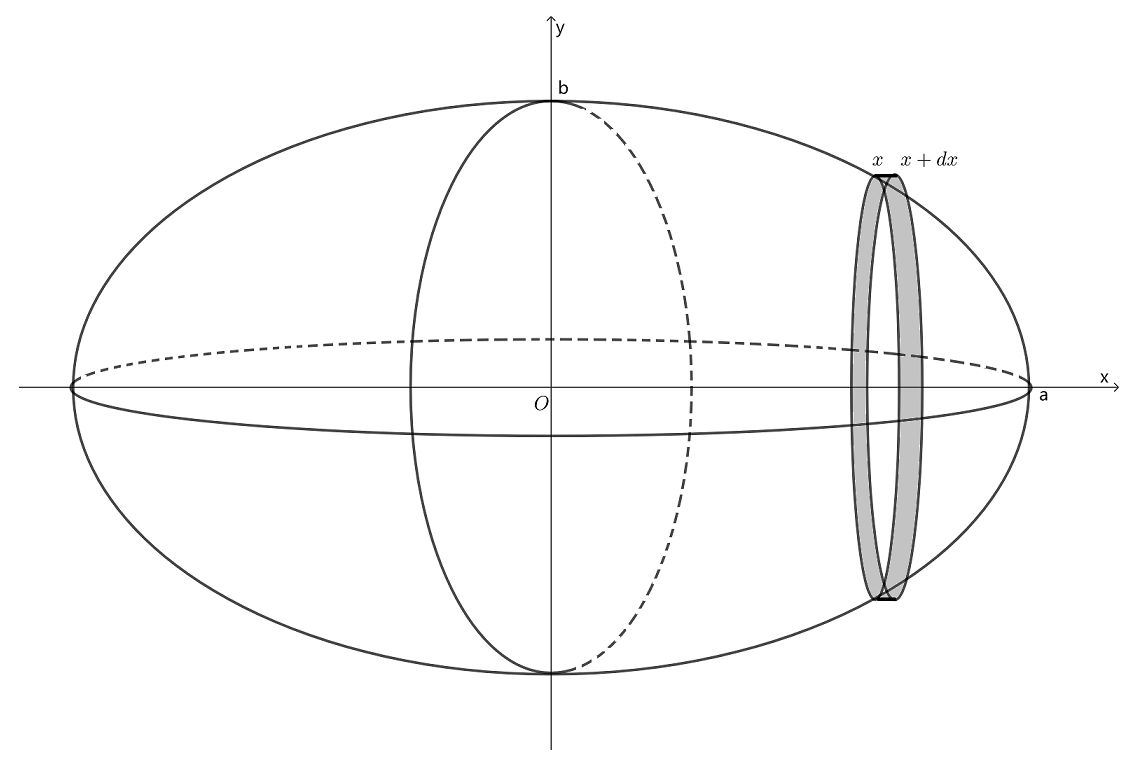
使用上一题中的方法计算它的体积,取半个椭圆
为积分变量,变化区间为 ,旋转椭球体中任意一小区间 对应的薄片的体积近似为半径为 ,高为 的圆柱体的体积,体积元素为:
于是旋转椭球体的体积为
A.
B.
C.
D.

 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App第2291题:椭球体体积
下图是由椭圆
所围成的图形绕x轴旋转一周而成的旋转椭球体.

使用上一题中的方法计算它的体积,取半个椭圆
为积分变量,变化区间为 ,旋转椭球体中任意一小区间 对应的薄片的体积近似为半径为 ,高为 的圆柱体的体积,体积元素为:
于是旋转椭球体的体积为
A.
B.
C.
D.
 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App