第2212题:三维空间中的有向面积
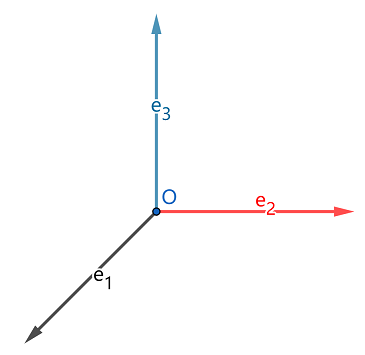
如上图,在向量空间 R3 中有三个满足右手规则的自然基,e1,e2,e3 . 假设在 R3 中有两个三维向量 b=⎣⎡b1b2b3⎦⎤ , c=⎣⎡bc1c2c3⎦⎤ ,它们所围成的三维空间中的有向面积为 S=b×c ,则( ).
A. S=∣∣∣∣b1b2c1c2∣∣∣∣e1 +∣∣∣∣b2b3c2c3∣∣∣∣e2+∣∣∣∣b3b1c3c1∣∣∣∣e3
B. S=∣∣∣∣b1b2c1c2∣∣∣∣e2 +∣∣∣∣b2b3c2c3∣∣∣∣e3+∣∣∣∣b3b1c3c1∣∣∣∣e1
C. S=∣∣∣∣b1b2c1c2∣∣∣∣e3 +∣∣∣∣b2b3c2c3∣∣∣∣e2+∣∣∣∣b3b1c3c1∣∣∣∣e1
D. S=∣∣∣∣b1b2c1c2∣∣∣∣e3 +∣∣∣∣b2b3c2c3∣∣∣∣e1+∣∣∣∣b3b1c3c1∣∣∣∣e2
注:可用 S=∣∣∣∣∣∣e1e2e3b1b2b3c1c2c3∣∣∣∣∣∣=0 来帮助记忆,其中第一列是自然基向量.


 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App
 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App