第2296题：空间曲线

考虑空间曲线，设其参数方程为

$\begin{cases} x=x(t), \\ y=y(t), \\ z=z(t) \end{cases}$ $(\alpha \leqslant t \leqslant \beta)$

若$x'(t)$ ，$y'(t)$ ，$z'(t)$ 在 $[\alpha,\beta]$ 上连续且不同时为零，则其弧长为

$s=$ $\int_{\alpha}^{\beta} \sqrt{[x'(t)]^2+[y'(t)]^2+[z'(t)]^2} dt$ .

空间螺旋线

$\begin{cases} x=a \cos t, \\ y=a \sin t, \\ z=c t \end{cases}$

的图形如下：

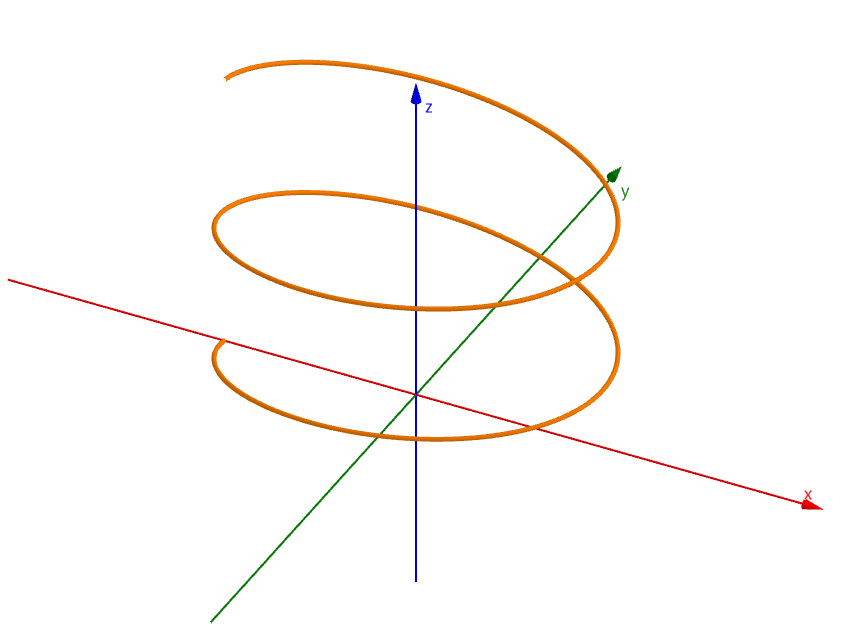
计算此螺丝旋线在区间 $[0,2\pi]$ 内的一段弧长.

A. $2 \pi (a+c)$

B. $2 \pi (a^2+c^2)$

C. $2 \pi \sqrt{a+c}$

D. $2 \pi \sqrt{a^2+c^2}$