第2243题：主轴定理

主轴定理：对于一个 $n \times n$ 对称矩阵 $A$ ，存在一个正交变量变换 $\bold{x}=P \bold{y}$ ，它将二次型 $\bold{x}^T A \bold{x}$ 变换为不含交叉项的二次型（标准型）$\bold{y}=D \bold{y}$ .

定理中矩阵 $P$ 的列称为二次型 $\bold{x}^T A \bold{x}$ 的主轴，向量 $\bold{y}$ 是向量 $\bold{x}$ 在由这些主轴构造的 $\mathbb{R} ^n$ 空间的单位正交基下的坐标向量.

定理中的 $D$ ，可由 $A$ 的特征值构建，$P$ 可由A的特征值对应的单位向量构建.

由于 $P$ 是由 $A$ 的不同特征值对应的特征向量构成的，所以 $P$ 一定是正交矩阵，因此有 $P^T=P^{-1}$ .

得到：

$A=PDP^{-1}$

$D=P^{-1}AP=P^TAP$

所以：

 $\bold{x}^T A \bold{x}=(P \bold{y})^T A (P \bold{y})$

$=\bold{y}^T P^T A P \bold{y}$

$=\bold{y}^T D \bold{y}$

其转换过程如下图

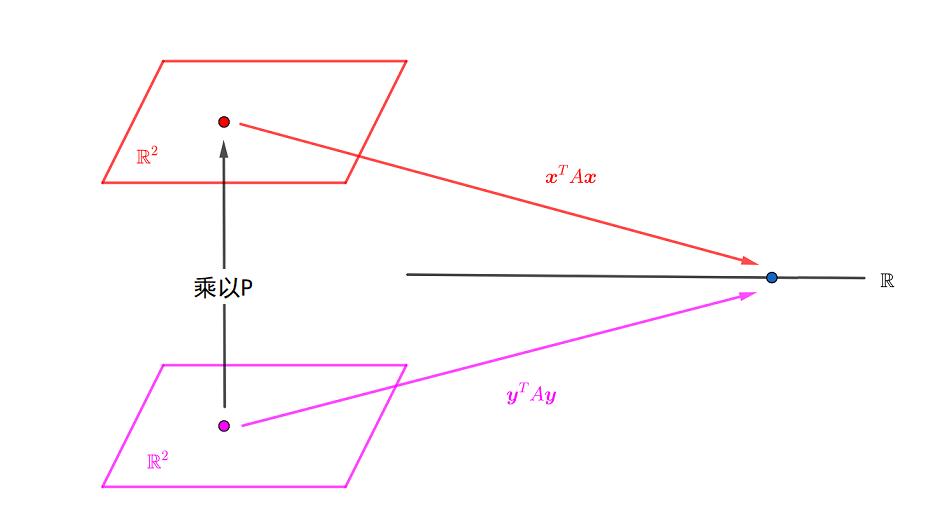
求一个变量代换矩阵 $P$ ，使得 $\bold{y}=P^{-1} \bold{x}=P^T \bold{x}$ ，可将由对称矩阵 $A=\begin{bmatrix} 9 & -2 \\ -2 & 6 \end{bmatrix}$ 构成的二次型 $M(\bold{x})=$ $9x_1^2-4x_1 x_2 +6x_2 ^2$ 变为一个没有交叉项的二次型$N(\bold{y})=ay_1^2 + by_2^2$ ，其中$a$ ，$b$ 为矩阵 $A$ 的特征值.

A.

$P=\begin{bmatrix} \dfrac{3}{\sqrt{5}} & -\dfrac{1}{\sqrt{5}} \\ \dfrac{1}{\sqrt{5}} & \dfrac{3}{\sqrt{5}} \end{bmatrix}$

B.

$P=\begin{bmatrix} \dfrac{2}{\sqrt{5}} & \dfrac{1}{\sqrt{5}} \\ -\dfrac{1}{\sqrt{5}} & \dfrac{2}{\sqrt{5}} \end{bmatrix}$

C.

$P=\begin{bmatrix} \dfrac{2}{\sqrt{7}} & -\dfrac{1}{\sqrt{7}} \\ \dfrac{1}{\sqrt{7}} & \dfrac{2}{\sqrt{7}} \end{bmatrix}$

D.

$P=\begin{bmatrix} \dfrac{4}{\sqrt{7}} & \dfrac{1}{\sqrt{7}} \\ -\dfrac{1}{\sqrt{7}} & \dfrac{4}{\sqrt{7}} \end{bmatrix}$