第2282题：阿基米德螺线

阿基米德螺线的极坐标方程为

$\rho =a +b \theta$

当 $a=0$ ，$b=1$ 时，其图形如下（ $0 \leqslant \theta \leqslant 2 \pi$ ）

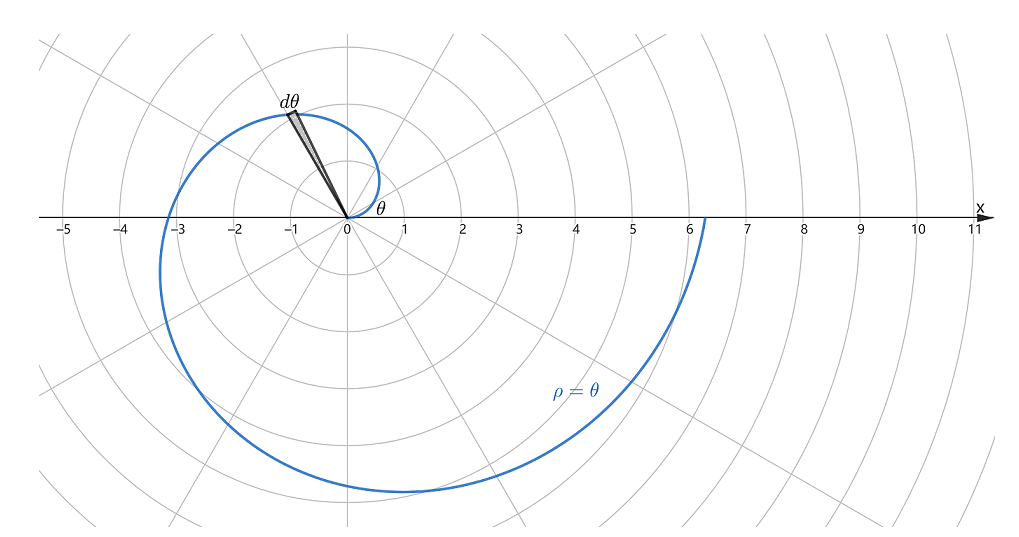
其极径 $\rho$ 随极角 $\theta$ 的改变而改变，不能用扇形面积公式 $S=\dfrac{1}{2}R^2 \theta$ 计算其面积。当取一极小角 $\theta$ 做为积分变量时，这一小区域的窄曲边扇形的面积可以用半径为$\rho=a+b\theta$ ，中心角为 $d\theta$ 的扇形面积来近似代替,那么有

$dS=$ $\dfrac{1}{2}[a+b\theta]^2 d\theta$

当 $\theta$ 在 $[\alpha,\beta]$ 区间时，阿基米德曲线扫过的面积为定积分

$\int_{\alpha}^{\beta} \dfrac{1}{2}[a+b\theta]^2 d\theta$ .

请计算阿基米德螺线

$\rho=3\theta$

在 $[0,2\pi]$ 区间内极径 $\rho$ 扫过的面积

$\int_{0}^{2\pi} \dfrac{1}{2}[3\theta]^2 d\theta$ .

A. $\dfrac{4}{3} \pi^3$

B. $4\pi^3$

C. $12 \pi^3$

D. $36 \pi^3$