第2242题:正交投影
考虑 Rn 中一个向量 y 分解为两个向量之和的问题,一个向量是向量 u 的数量积 au ,另一个向量是与 u 垂直的向量 z ,如下图.
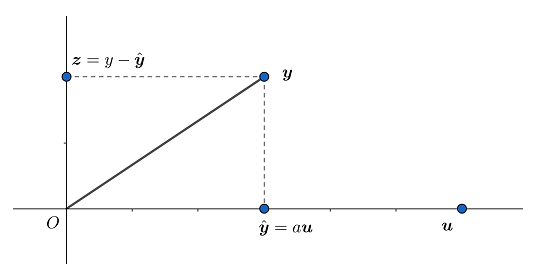
我们期望写成 z=y−y^
y=y^+z
其中 y^=au ( y^ 可念作 y-hat,或y-帽),a 是一个数.
z=y−y^ ,与 u 正交的充分必要条件是
(y−au)⋅u
=y⋅u−a(u⋅u)
=0
得到 a=u⋅uy⋅u
y^=u⋅uy⋅u⋅u
向量 y^ 称为 y 在 u 上的正交投影,向量 z 称为 y 垂直于u 的分量.
设 y=[63] ,u=[26] ,
求 y 在 u 上的正交投影 y^ .
A. y^=⎣⎢⎢⎡2329⎦⎥⎥⎤
B. y^=⎣⎢⎢⎡4349⎦⎥⎥⎤
C.y^=⎣⎢⎢⎡3437⎦⎥⎥⎤
D. y^=⎣⎢⎢⎡3267⎦⎥⎥⎤



