第2292题:随球面的体积
上一题中的旋转椭球体在垂直于 轴方向上的切面都是圆,如果这个切面也是一个椭圆,如下图,被称为椭球面
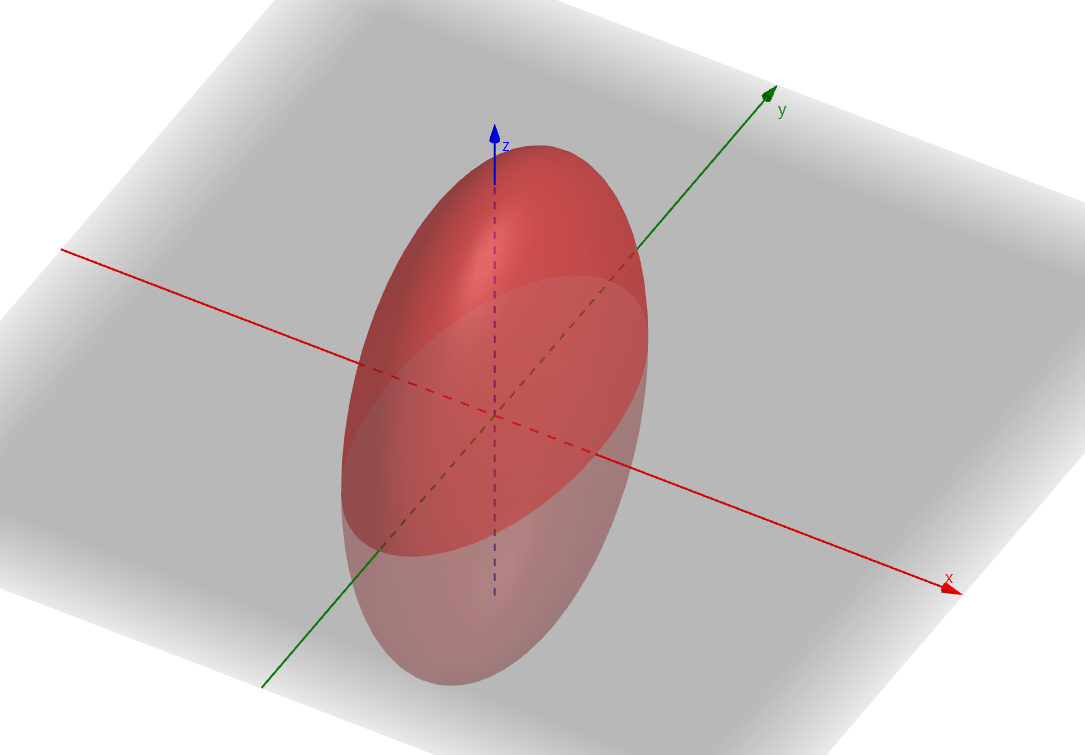
椭球面的方程为
根据上一题的结果,推测一下此椭球面的体积是多少?
A.
B.
C.
D.
注:用垂直于 轴的平面截椭球面得到的截痕为一椭圆,它在 平面上的投影为
所以其半轴分别为
,
因此,此截椭圆的面积为
, -
所求椭球面的体积为
.

 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App第2292题:随球面的体积
上一题中的旋转椭球体在垂直于 轴方向上的切面都是圆,如果这个切面也是一个椭圆,如下图,被称为椭球面

椭球面的方程为
根据上一题的结果,推测一下此椭球面的体积是多少?
A.
B.
C.
D.
注:用垂直于 轴的平面截椭球面得到的截痕为一椭圆,它在 平面上的投影为
所以其半轴分别为
,
因此,此截椭圆的面积为
, -
所求椭球面的体积为
.
 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App