第2219题：矩阵的病态程度

在实际工作中，常会遇到“接近奇异的”或者“病态”的矩阵. 一个非奇异矩阵（可逆矩阵），当它的某些元素稍微改变就变成奇异矩阵（不可逆矩阵）, 有时舍入误差即可能导致方程不可解. 为了研究线性方程组近似解的误差估计，需要对 $\mathbb{R}^n$ 中向量或矩阵的“大小”引进一种度量：范数(norm).

范数定义了向量空间里的距离，它的出现使得向量之间的比较成为了可能，可以这样简单的理解范数：通过某种算法 $f(x)$ 把一组实数(向量)映射成一个实数，这个实数就是范数，有时也称这个映射算法 $f(x)$ 为范数.

例如，在 $\mathbb{R}^2$ 中有向量 $\lambda=(2,2)^T$ ，其 $L_1$ 范数为 $4$ ，$L_2$ 范数为 $2\sqrt{2}$ ，如下图：

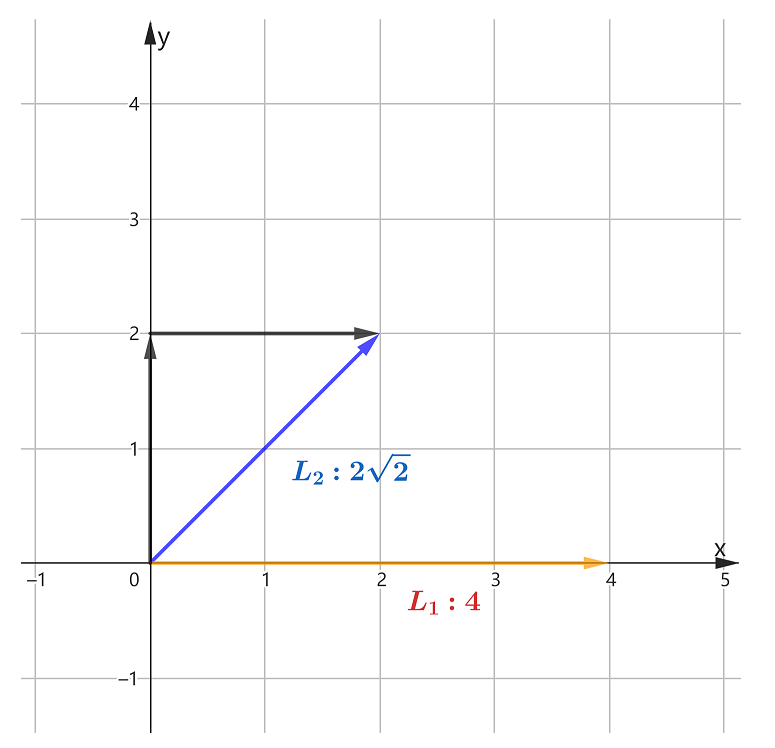
其中 $L_1$ 范数，也叫曼哈顿距离：是向量中所有元素的绝对值之和.

$L_2$ 范数，也叫欧几里得距离，是向量中所有元素的平方和，再开平方.

矩阵的范数类似. 进而有条件数（cond）的定义，矩阵 $A$ 的条件数等于 $A$ 的范数与其逆矩阵 $A^{-1}$ 的范数的乘积，条件数是判断矩阵病态与否的一种度量，条件数越大矩阵越病态.

请计算向量 $\bold{\alpha}=(1,2,2,4)^T$ 的 $L_2$ 范数.