第2345题:悬链线
如下图,
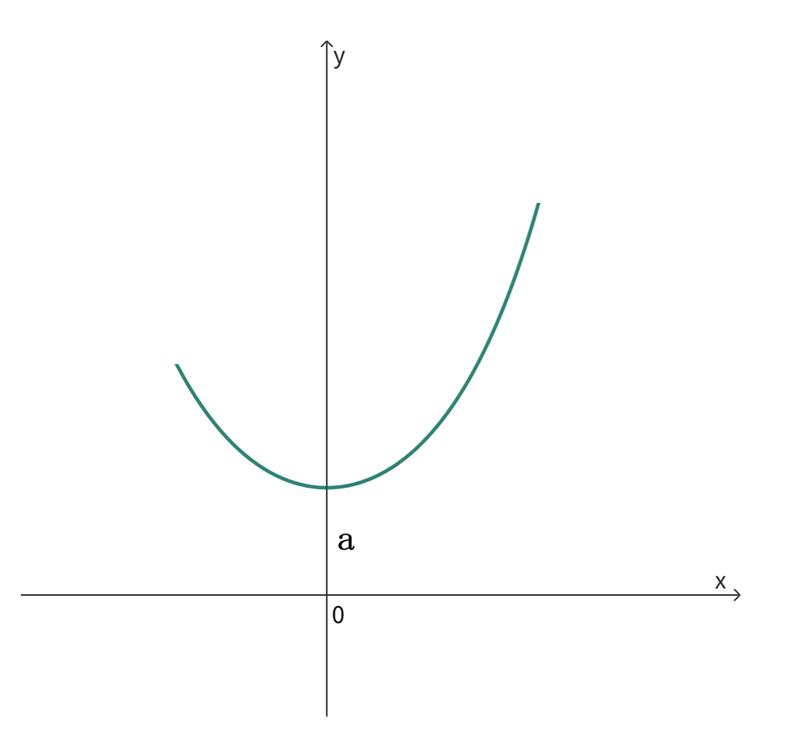
设有一根均匀、柔软的绳索,两端固定,绳索仅受重力的作用而下垂,该绳索在平衡状态时的曲线叫做悬链线,悬链线的微分方程为:
其中, 为绳索最底端与坐标原点间的距离。求当初值条件为
,
时,此微分方程的特解.
A.
B.
C.
D.

 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App第2345题:悬链线
如下图,

设有一根均匀、柔软的绳索,两端固定,绳索仅受重力的作用而下垂,该绳索在平衡状态时的曲线叫做悬链线,悬链线的微分方程为:
其中, 为绳索最底端与坐标原点间的距离。求当初值条件为
,
时,此微分方程的特解.
A.
B.
C.
D.
 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App