第2287题：旋转抛物体体积

下图是抛物线 $y^2=2px$ 绕x轴旋转所得旋转抛物体。

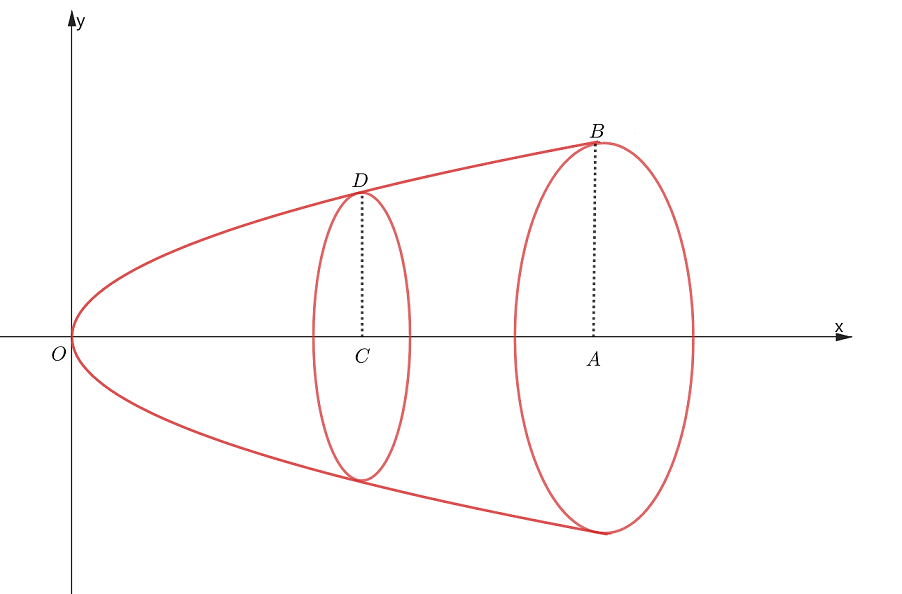
设旋转抛物体的高 $OA=H$ ，与上一题相似，取 $x$ 为积分变量，变化区间为 $[0,H]$ ，旋转抛物体中任意一小区间 $[x,x+dx]$ 对应的薄片的体积近似为半径为 $y= \sqrt{2px}$ ，高为 $dx$ 的圆柱体的体积，体积元素为：

$dV=\pi ( \sqrt{2px})^2 dx$

于是旋转抛物体的体积为

$V_{\text{旋转抛物体}}=$$\int_0^H \pi ( \sqrt{2px})^2 dx$ $=\pi p H^2$ .

令旋转抛物体的底面积为 $S$ ，同底同高圆柱体的体积 $V_{\text{圆柱体}}=SH$ ，得到旋转抛物体体积和同底同高圆柱体的体积之间的关系为（ ）.

A. $V_{\text{旋转抛物体}}=$ $\dfrac{V_{\text{圆柱体}}}{2}$

B. $V_{\text{旋转抛物体}}=$ $\dfrac{V_{\text{圆柱体}}}{3}$

C. $V_{\text{旋转抛物体}}$ $=\dfrac{V_{\text{圆柱体}}}{4}$

D.$V_{\text{旋转抛物体}}$ $=\dfrac{\sqrt{V_{\text{圆柱体}}}}{4}$