第2240题:旋转变换与辐角
设矩阵 C=[ab−ba] ,其中 a,b 为实数且不都等于零,C 的特征值是 λ=a±bi .
设 r=∣λ∣=√a2+b2 ,则有
C=r⎣⎢⎡rarb−rbra⎦⎥⎤
如下图,在复平面上画出 a,b,r 三者的关系,其中角 ϕ 称为 λ=a±bi 的辐角,可以得到
ra=cosϕ
rb=sinϕ
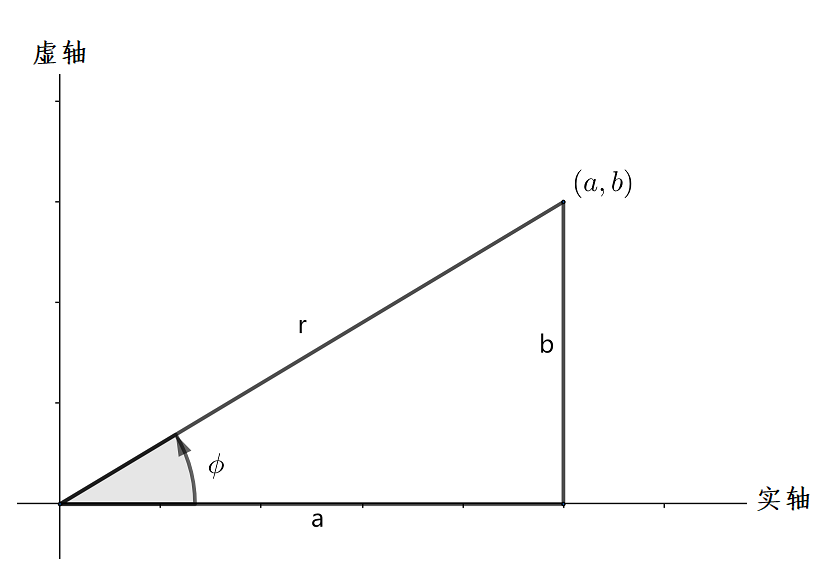
因此,
C=[r00r]⎣⎢⎡rarb−rbra⎦⎥⎤
=[r00r][cosϕsinϕ−sinϕcosϕ]
所以 C 是含有旋转变换的矩阵.
设 A=[√33−3√3]
求 A 的特征值的辐角是多少度?


 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App
 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App