面积原理例6
考察函数 ,当 时,它是凸函数.
如图1,连接两点 与 的弦必在相应曲线段的上方,因此图1中梯形的面积必大于曲边梯形的面积.
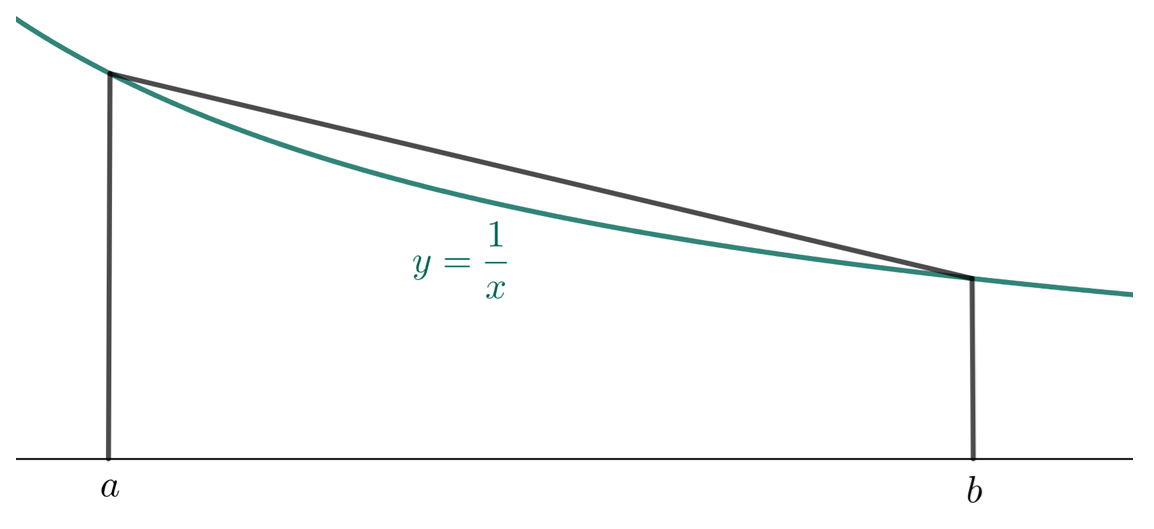
如图2,过曲线上点 作曲线的切线,它与 , 两线所围成的档形面积必小于曲边梯形的面积.
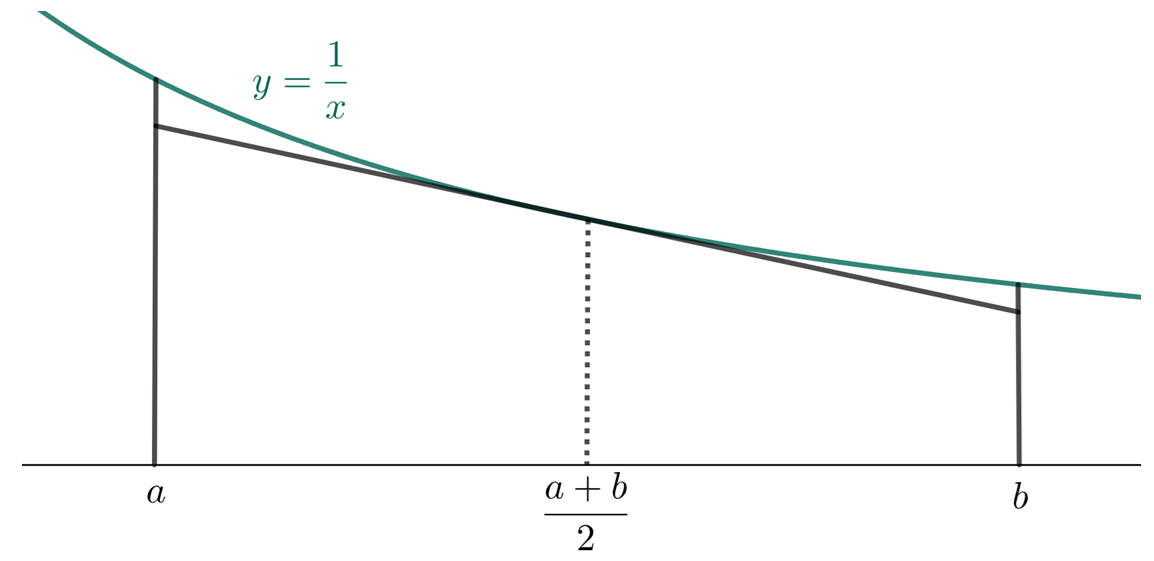
曲边梯形的面积为 .
由此,可得到不等式: .

 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App面积原理例6
考察函数 ,当 时,它是凸函数.
如图1,连接两点 与 的弦必在相应曲线段的上方,因此图1中梯形的面积必大于曲边梯形的面积.

如图2,过曲线上点 作曲线的切线,它与 , 两线所围成的档形面积必小于曲边梯形的面积.

曲边梯形的面积为 .
由此,可得到不等式: .
 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App