面积原理1

面积原理是一种利用定积分的几何意义来估计和式的方法. 对于单调函数，可以通过比较曲线下的面积（定积分）与矩形面积的和（和式）来建立不等式.

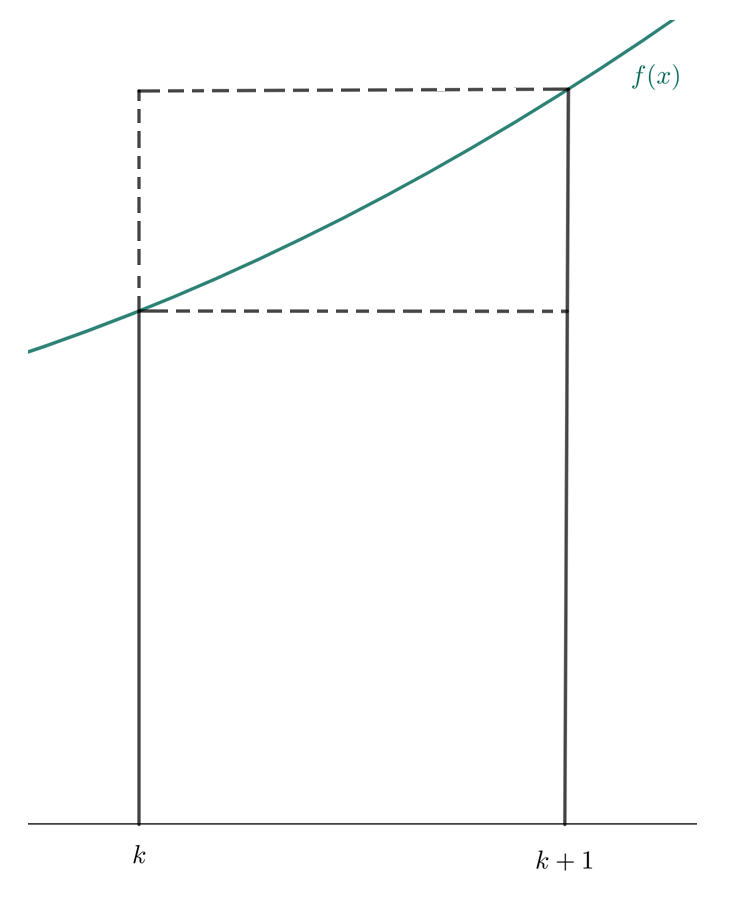
具体来说，如果函数 $f(x)$ 在区间 $[a,b]$ 上单调，那么和式 $\displaystyle\sum_{k=m}^n$ 可以用积分 来上下估计.

设 $f(x)$ 是定义在 $[1,\infty)$ 上的正单调递减函数，则对于整数 $n \geqslant 1$ 有：

$\int_1^n f(x)dx +f(n) \leqslant \displaystyle \sum_{k=1}^n f(k)$$\leqslant f(1)+\int_1^n f(x)dx$

对于单调递增函数，不等式方向相反.

面积原理常用于估计级数的部分和、证明不等式以及分析算法的复杂度.

调和级数 $H_n= \displaystyle \sum_{k=1}^n \dfrac{1}{k}$ 是发散的，但可以用面积原理来估计其增长阶.

考虑函数 $f(x)=\dfrac{1}{x}$ ，它的 $[1,\infty)$ 上单调递减，应用面积原理可知调和级数的部分和以对数速度增长，有

$\ln n +\dfrac{1}{n} \leqslant H_n \leqslant 1+\ln n$.