Young不等式

参考下图，设连续函数 $\varphi$ 在 $[0,+\infty)$ 上严格递增且过原点，那么必存在过原点的连续反函数$\phi$ ，且在$[0,\varphi(+\infty))$ 上严格递增. 参考下图

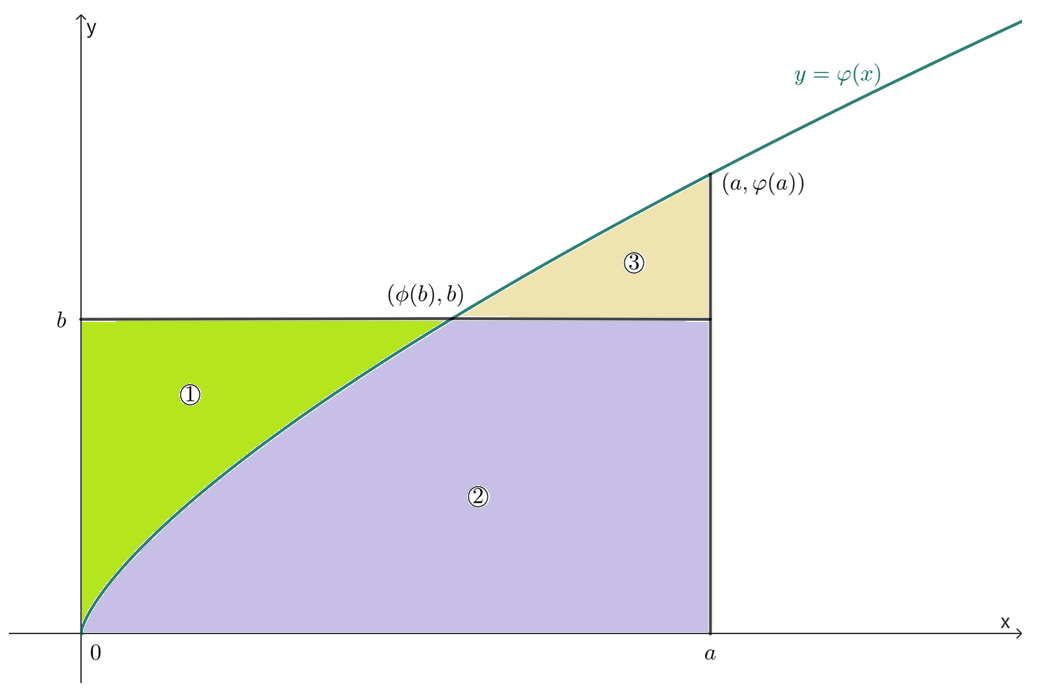
对于定义域内的$a,b$ ，有以下面积关系：

①+②$=ab$

②+③$=\int_0^a \varphi(x) dx$

①$=\int_0^b \phi(y) dy$

于是得到Young不等式：

$ab \leqslant \int_0^a \varphi(x) dx +\int_0^b \phi(y) dy$

从图中可以得到等号成立的条件.

注：

● William Henry Young， 威廉·亨利·杨，1863年10月20日（伦敦）－ 1942年7月7日（瑞士洛桑）。

● 1896年，他与 Grace Chisholm Young 结婚。Grace 是英国第一位正式获得数学博士学位的女性（在哥廷根大学，师从菲利克斯·克莱因）。

● 他们的婚姻是科学史上著名的合作夫妻之一，合写了大量数学论文。

● 由于当时英国学术界的性别歧视，很多成果以 W. H. Young 的名义发表，但据信许多思想来自夫妻共同讨论，甚至主要由 Grace 完成。后来他公开承认妻子的巨大贡献。